Ричард Фейнман - Том 2. Электромагнетизм и материя

Чтобы мысль была яснее, рассмотрим только одномерный случай. Представим себе коллоидную частицу в виде очень большого (по сравнению с атомом!) шара; тогда мы можем малую часть ее поверхности считать плоскостью. (Вообще, пытаясь понять новое явление, лучше разобраться в нем на чрезвычайно упрощенной модели; и только потом, поняв суть проблемы, стоит браться за более точные расчеты.)

Предположим, что распределение ионов создает плотность зарядов ρ( х ) и электрический потенциал φ, связанные электростатическим законом ∇ 2φ=-ρ/ε 0, или в одномерном случае законом

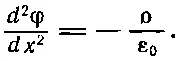(7.28)

Как бы распределились ионы в таком поле, если бы потенциал подчинялся этому уравнению? Узнать это можно при помощи принципов статистической механики. Вопрос в том, как определить φ, чтобы вытекающая из статистической механики плотность заряда тоже удовлетворяла бы условию (7.28)?

Согласно статистической механике (см. вып. 4, гл. 40), частицы, пребывая в тепловом равновесии в поле сил, распределяются так, что плотность n частиц с координатой x дается формулой

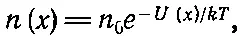(7.29)

где U ( x ) — потенциальная энергия, k — постоянная Больцмана, а Т — абсолютная температура.

Предположим, что у всех ионов один и тот же электрический заряд, положительный или отрицательный. На расстоянии х от поверхности коллоидной частицы положительный ион будет обладать потенциальной энергией

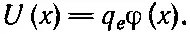
Плотность положительных ионов тогда равна

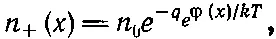
а плотность отрицательных

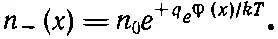
Суммарная плотность заряда

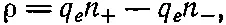
или

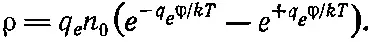(7.30)

Подставляя в (7.28), увидим, что потенциал φ должен удовлетворять уравнению

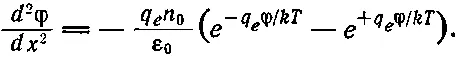(7.31)

Это уравнение решается в общем виде [помножьте обе его части на 2(dφ/dx) и проинтегрируйте по х], но, продолжая упрощать задачу, мы ограничимся здесь только предельным случаем малых потенциалов или высоких температур Т . Малость φ отвечает разбавленному раствору. Показатель экспоненты тогда мал, и можно взять

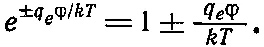(7.32)

Уравнение (7.31) дает

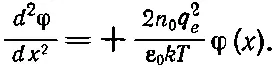(7.33)

Заметьте, что теперь в правой части стоит знак плюс (решение не колебательное, а экспоненциальное).

Общее решение (7.33) имеет вид

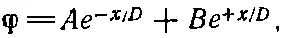(7.34)

где

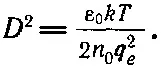(7.35)

Постоянные А и В определяются из добавочных условий. В нашем случае В должно быть нулем, иначе потенциал для больших х обратится в бесконечность. Итак,

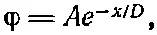(7.36)

где А — потенциал при x=0 на поверхности коллоидной частицы.

Потенциал убывает в e раз при удалении на D (фиг. 7.7).

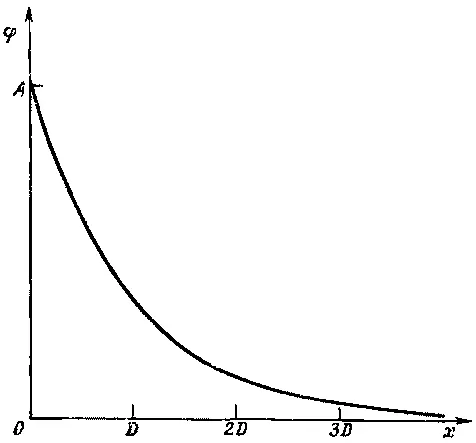
Фиг. 7.7. Изменение потенциала у поверхности коллоидной частицы. D — дебаевская длина.

Число D называется дебаевской длиной ; это мера толщины ионной оболочки, окружающей в электролите каждую большую заряженную частицу. Уравнение (7.36) утверждает, что оболочка становится тоньше по мере увеличения концентрации ионов (n 0) или уменьшения температуры.

Постоянную А в (7.36) легко получить, если известен поверхностный заряд а на поверхности заряженной частицы. Мы знаем, что

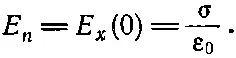(7.37)

Но Е это также градиент φ

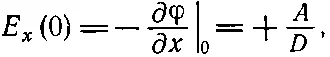(7.38)

откуда получается

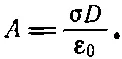(7.39)

Подставив этот результат в (7.36), мы получим (положив х =0), что потенциал коллоидной частицы равен

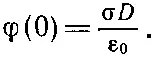(7.40)

Заметьте, что этот потенциал совпадает с разностью потенциалов в конденсаторе с промежутком D и поверхностной плотностью заряда σ.

Мы сказали, что коллоидные частицы не слипаются вследствие электрического отталкивания. Но теперь мы видим, что невдалеке от поверхности частицы из-за возникающей вокруг нее ионной оболочки поле спадает. Если бы оболочка стала достаточно тонкой, у частиц появился бы шанс столкнуться друг с другом. Тогда они бы слиплись, коллоид бы осадился и выпал из жидкости. Из нашего анализа ясно, что после добавления в коллоид подходящего количества соли начнется выпадение осадка. Этот процесс называется «высаливанием коллоида».

Другой интересный пример — это влияние растворения соли на осаждение белка. Молекула белка — это длинная, сложная и гибкая цепь аминокислот. На ней там и сям имеются заряды, и временами заряд какого-то одного знака, скажем отрицательного, распределяется вдоль всей цепи. В результате взаимного отталкивания отрицательных зарядов белковая цепь распрямляется. Если в растворе имеются еще другие такие же молекулы-цепочки, то они не слипаются между собой вследствие того же отталкивания. Так возникает в жидкости взвесь молекул-цепочек. Но стоит добавить туда соли, как свойства взвеси изменятся. Уменьшится дебаевская длина, молекулы начнут сближаться и свертываться в спирали. А если соли много, то молекулы белка начнут выпадать в осадок. Существует множество других химических явлений, которые можно понять на основе анализа электрических сил.