Ричард Фейнман - Том 2. Электромагнетизм и материя

Для примера посмотрим, к какой физической задаче приведет нас функция Р ( ℨ )= ℨ 2. Из нее мы получаем две потенциальные функции (7.5) и (7.6). Чтобы увидеть, какую задачу решает функция U , мы найдем эквипотенциальные поверхности, полагая U равным постоянному числу А :

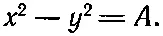
Это уравнение прямоугольной гиперболы. Перебирая разные значения А , мы получаем семейство гипербол, начерченное на фиг. 7.1. Когда A=0, то гиперболы вырождаются в пару диагоналей, проходящих через начало.

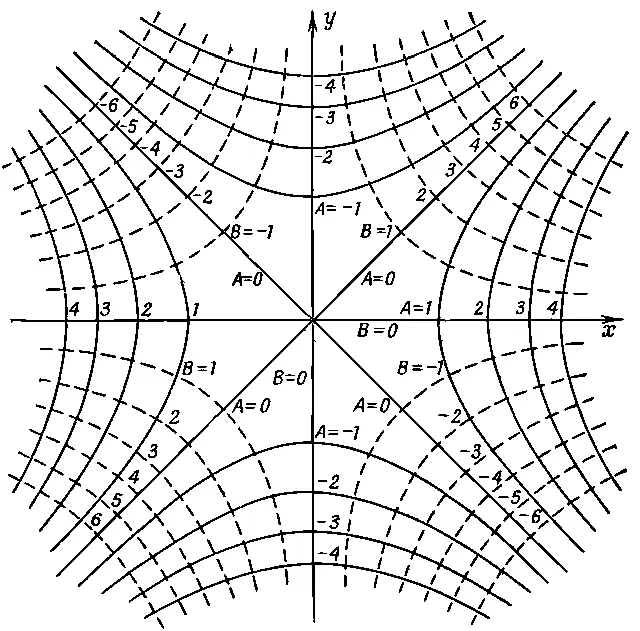
Фиг. 7.1. Два семейства ортогональных кривых, которые могут представлять собой эквипотенциальные линии двумерного электростатического поля.

Такое семейство эквипотенциальных поверхностей встречается в нескольких физических задачах. В одной из них оно изображает детали структуры поля возле точки между двумя одинаковыми точечными зарядами. В другой оно изображает поле внутри прямого угла, образованного двумя проводящими плоскостями. Если есть два электрода, изогнутых так, как показано на фиг. 7.2, и имеющих разные потенциалы, то поле внутри угла С будет выглядеть в точности так же, как поле около начала координат на фиг. 7.1.

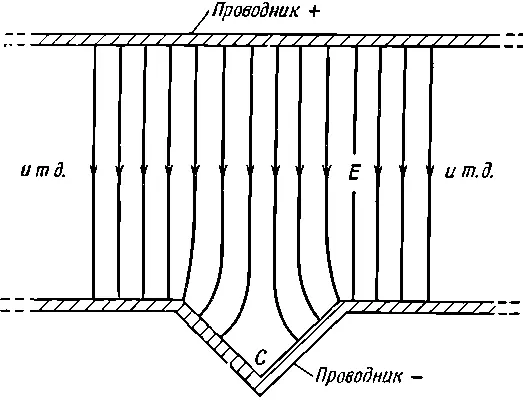
Фиг. 7.2. Поле возле точки С такое же, как на фиг. 7.1.

Сплошные линии — это эквипотенциальные поверхности, а пересекающие их штриховые — это линии поля Е. Вблизи острия или выступа электрическое поле повышается, а возле впадины или отверстия оно слабеет.

Найденное нами решение отвечает также гиперболическому электроду, помещенному около прямого угла, или двум гиперболам при соответствующих потенциалах. Заметьте, что поле фиг. 7.1 имеет интересное свойство. Составляющая х электрического поля Едается выражением

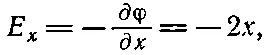
т. е. электрическое поле пропорционально расстоянию от оси координат. Этот факт был использован, чтобы создать устройство (называемое квадрупольной линзой), необходимое для фокусирования пучков частиц (см. вып. 6, гл. 29, § 9). Фокусирующее поле обычно получают с помощью четырех гиперболических электродов, изображенных на фиг. 7.3.

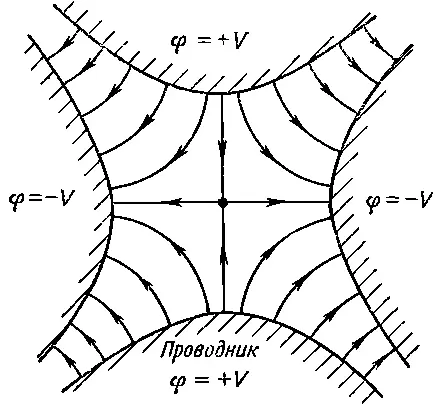
Фиг. 7.3. Поле квадрупольной линзы.

Проводя здесь линии электрического поля, мы просто перечертили с фиг. 7.1 семейство штриховых кривых V=const. Эти линии достались нам совершенно бесплатно! Кривые V=const перпендикулярны к кривым U =const, как это следует из уравнений (7.7) и (7.8). Как только мы выбираем функцию F ( ℨ ), то получаем из U и V сразу же эквипотенциальные линии и линии поля. Мы давно знаем, что можно решить на выбор любую из двух задач, смотря по тому, какое семейство кривых мы примем за эквипотенциальное.

Другим примером послужит функция

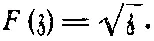(7.11)

Если мы напишем

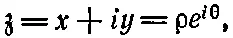
где

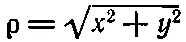
и

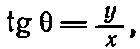
то

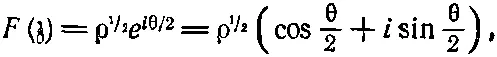
откуда следует

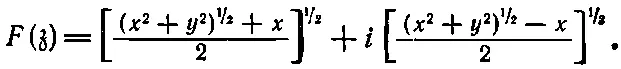(7.12)

Кривые U ( х, у )= А и V ( х, у )= В , где U и V взяты из уравнения (7.12), проведены на фиг. 7.4.

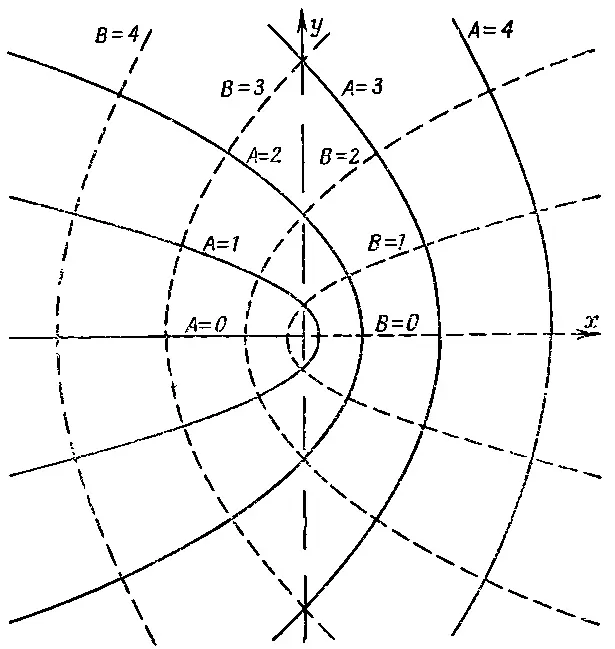
Фиг. 7.4. Кривые постоянных U(x, у) и V(x, у) ив уравнения (7.12).

И здесь тоже можно назвать немало случаев, описываемых этими полями. Один из самых интересных — это поле у края тонкой пластинки. Если линия В =0 направо от оси у изображает тонкую заряженную пластину, то линии поля близ нее даются кривыми с различными А. Физическая картина показана на фиг. 7.5.

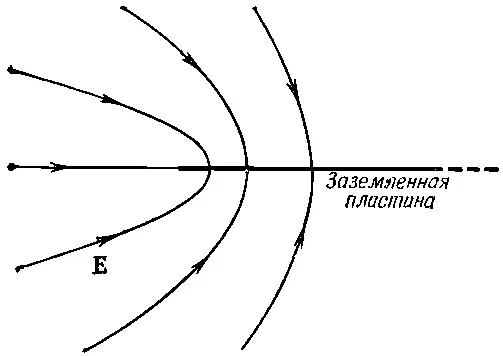
Фиг. 7.5. Электрическое поле возле края тонкой заземленной пластины.

Дальнейшие примеры — это функция

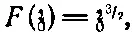(7.13)

дающая нам поле снаружи прямого угла, функция

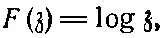(7.14)

дающая поле заряженной нити, и функция

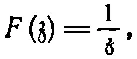(7.15)

изображающая поле двумерного аналога электрического диполя, т. е. двух параллельных прямых, заряженных противоположным знаком и помещенных вплотную друг к другу.

Больше этим вопросом в нашем курсе мы заниматься не будем; мы должны только подчеркнуть, что, хотя техника комплексных переменных часто оказывается очень мощной, она ограничена все же только двумерными задачами; к тому же это все-таки косвенный метод.

Займемся теперь такими физическими задачами, в которых поле создается не закрепленными зарядами и не зарядами на проводящих поверхностях, а сочетанием обоих факторов. Иными словами, полем управляют одновременно две системы уравнений: 1) уравнения электростатики, связывающие электрическое поле с распределением зарядов; 2) уравнения из другой области физики, определяющие положение или движения зарядов в поле.

Сперва мы разберем один динамический пример. В нем движение зарядов контролируется законами Ньютона. Простой пример такого положения вещей наблюдается в плазме, в ионизованном газе, состоящем из ионов и свободных электронов, распределенных в какой-то области пространства. Ионосфера (верхний слой атмосферы) служит примером такой плазмы. Ультрафиолетовые лучи Солнца отрывают от молекул воздуха электроны и создают свободные электроны и ионы. В плазме положительные ионы намного тяжелее электронов, так что можно пренебречь движением в ней ионов по сравнению с движением электронов.

Пусть n 0будет плотностью электронов в невозмущенном равновесном состоянии. Такой же должна быть и плотность положительных ионов, потому что в невозмущенном состоянии плазма нейтральна. Теперь допустим, что электроны каким-то образом выведены из равновесия. Что тогда получится? Если плотность электронов в какой-то области возросла, они начнут отталкиваться и стремиться вернуться в прежнее положение равновесия. Двигаясь к своим первоначальным положениям, они наберут кинетическую энергию и вместо того, чтобы замереть в равновесной конфигурации, проскочат мимо. Начнутся колебания. Нечто похожее наблюдается в звуковых волнах, но там возвращающей силой было давление газа. В плазме возвращающая сила — это действующее на электроны электрическое притяжение.