Ричард Фейнман - Том 2. Электромагнетизм и материя

Чтобы упростить рассуждения, мы будем заниматься только одномерным движением электронов — скажем, в направлении x. Предположим, что электроны, первоначально находившиеся в точке х , к моменту t сместились из положения равновесия на расстояние s ( x, t ). Раз они сместились, то плотность их, вообще говоря, изменилась. Это изменение подсчитать легко. Если посмотреть на фиг. 7.6, то видно, что электроны, вначале находившиеся между плоскостями а и b, сдвинулись и теперь находятся между плоскостями а' и b'. Количество электронов между а и b прежде было пропорционально n 0Δ х ; теперь то же их количество находится в промежутке шириной Δx+Δs.

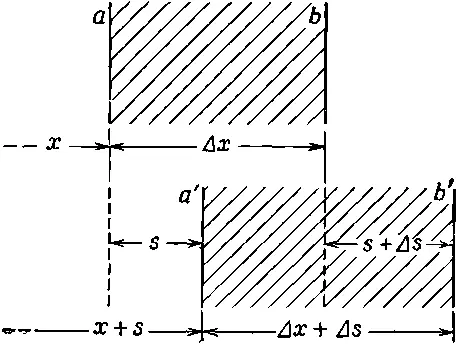
Фиг. 7.6. Движение волны в плазме. Электроны от плоскости а сдвигаются к а', а от b —к b'.

Плотность теперь стала

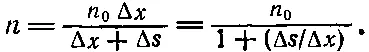(7.16)

Если изменение плотности мало, то можно написать [заменяя с помощью биномиального разложения (1+ε) -1на (1-ε)]

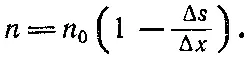(7.17)

Что касается ионов, то предположим, что они не сдвинулись заметно с места (инерция-то у них куда больше), так что плотность их осталась прежней, n 0. Заряд каждого электрона -q e , и средняя плотность заряда в любой точке равна

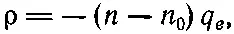
или

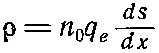(7.18)

(здесь Δs/Δx записано через дифференциалы).

Далее, уравнения Максвелла связывают с плотностью зарядов электрическое поле. В частности,

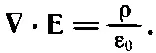(7.19)

Если задача действительно одномерна (и никаких полей, кроме вызываемых смещением электронов, нет), то у электрического поля Еесть одна-единственная составляющая Е х . Уравнение (7.19) вместе с (7.18) приведет к

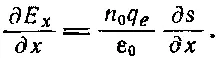(7.20)

Интегрируя (7.20), получаем

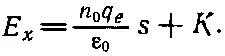(7.21)

Постоянная интегрирования К равна нулю, потому что Е х =0 при s=0.

Сила, действующая на смещенный электрон, равна

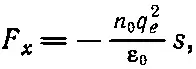(7.22)

т. е. возвращающая сила пропорциональна смещению s электрона. Это приведет к гармоническим колебаниям электронов. Уравнение движения смещенного электрона имеет вид

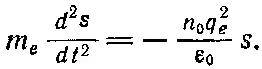(7.23)

Отсюда следует, что s меняется по гармоническому закону. Во времени s меняется как cos ωt или, если использовать экспоненту (см. вып. 3), как

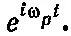(7.24)

Частота колебаний ω р определяется из (7.23):

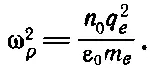(7.25)

Это число, характеризующее плазму, называют собственной частотой колебаний плазмы , или плазменной частотой .

Оперируя с электронами, многие предпочитают получать ответы в единицах e 2, определяемых как

(7.26)

При этом условии (7.25) превращается в

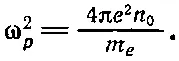(7.27)

В таком виде эту формулу можно встретить во многих книгах.

Итак, мы обнаружили, что возмущения плазмы приводят к свободным колебаниям электронов вблизи положения равновесия с собственной частотой ω р , пропорциональной корню квадратному из плотности электронов. Плазменные электроны ведут себя как резонансная система, подобная описанным в вып. 2, гл. 23.

Этот собственный резонанс плазмы приводит к интересным эффектам. Например, при прохождении радиоволн сквозь ионосферу обнаруживается, что они могут пройти только в том случае, если их частота выше плазменной частоты. А иначе они отражаются обратно. Для связи с искусственным спутником мы используем высокие частоты. Если же мы хотим связаться с радиостанцией, расположенной где-то за горизонтом, то необходимы частоты меньшие, чем плазменная частота, иначе сигнал не отразится обратно к Земле.

Другой интересный пример колебаний плазмы наблюдается в металлах. В них содержится плазма из положительных ионов и свободных электронов. Плотность n 0там очень высока, значит, велика и ω р . Но колебания электронов все же можно обнаружить. Ведь, согласно квантовой механике, гармонический осциллятор с собственной частотой ω р обладает уровнями энергии, отличающимися друг от друга на величину ℏω р. Значит, если, скажем, обстреливать электронами алюминиевую фольгу и очень точно измерять их энергию по ту сторону фольги, то можно ожидать, что временами электроны будут из-за колебаний плазмы терять как раз энергию ℏ ω p . Так это и происходит. Впервые это явление наблюдалось экспериментально в 1936 г. Электроны с энергиями от нескольких сот до нескольких тысяч электронвольт, рассеиваясь от тонкой металлической фольги или проходя сквозь нее, теряли энергию порциями. Эффект оставался непонятым до 1953 г., пока Бом и Пайнс [8] О новых работах по этому вопросу и библиографию см. в статье С. J.Powell, J.B. Swann, Phys. Rev., 115, 869 (1959). не показали, что все это можно объяснить квантовым возбуждением плазмы в металле.

Обратимся к другому явлению, когда местоположение зарядов определяется потенциалом, создаваемым в какой-то степени самими зарядами. Такой эффект существен для поведения коллоидов. Коллоид — это взвесь маленьких заряженных частичек в воде. Хотя эти частички и микроскопические, но по сравнению с атомом они все же очень велики. Если бы коллоидные частицы не были заряжены, они бы стремились коагулировать (слиться) в большие комки; но, будучи заряженными, они отталкиваются друг от друга и остаются во взвешенном состоянии. Если в воде растворена еще соль, то она диссоциирует (расползается) на положительные и отрицательные ионы. (Такой раствор ионов называется электролитом.) Отрицательные ионы притягиваются к коллоидным частицам (будем считать, что их заряды положительны), а положительные — отталкиваются. Нам нужно узнать, как ионы, окружающие каждую частицу коллоида, распределены в пространстве.