Ричард Фейнман - Том 2. Электромагнетизм и материя

Представьте, что мы сооружаем шар, наслаивая последовательно друг на друга сферические слои бесконечно малой толщины. На каждой стадии процесса мы собираем небольшое количество электричества и размещаем его тонким слоем от r до r + dr . Мы продолжаем процесс этот до тех пор, пока не доберемся до заданного радиуса а (фиг. 8.2).

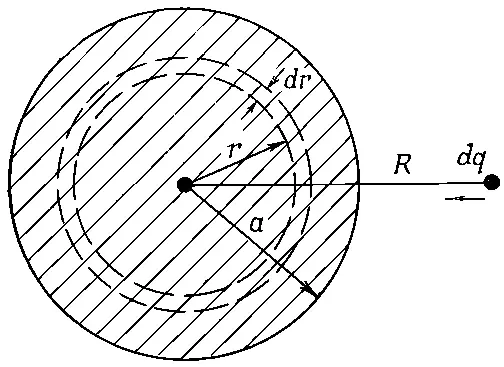
Фиг. 8.2. Энергию однородно заряженного шара можно рассчитать, вообразив, что его слепили, последовательно наслаивая друг на друга сферические слои.

Если Q r — это заряд шара в тот момент, когда шар доведен до радиуса r, то работа, требуемая для доставки на шар заряда dQ , равна

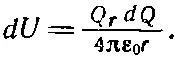(8.4)

Если плотность заряда внутри шара есть ρ, то заряд Q r равен

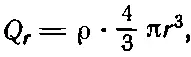
а заряд dQ равен

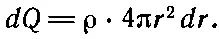
Уравнение (8.4) превращается в

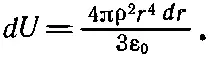(8.5)

Полная энергия, требуемая на то, чтобы накопить полный шар зарядов, равна интегралу по dU от r=0 до r=а, т.е.

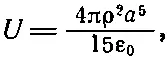(8.6)

а если мы желаем выразить результат через полный заряд Q шара, то

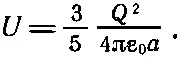(8.7)

Энергия пропорциональна квадрату полного заряда и обратно пропорциональна радиусу. Можно представить (8.7) и так: среднее значение (1/r ij) по всем парам точек внутри шара равно 6/ 5а.

Рассмотрим теперь энергию, требуемую на то, чтоб зарядить конденсатор. Если заряд Q был снят с одной обкладки конденсатора и перенесен на другую, то между обкладками возникает разность потенциалов, равная

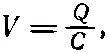(8.8)

где С — емкость конденсатора. Сколько работы затрачено на зарядку конденсатора? Поступая точно так же, как мы поступали с шаром, вообразим, что конденсатор уже заряжен переносом заряда с одной обкладки на другую маленькими порциями dQ . Работа, требуемая для переноса заряда dQ , равна

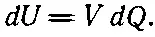
Взяв V из (8.8), напишем

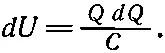
Или, интегрируя от Q =0 до конечного заряда Q , получаем

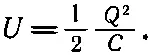(8.9)

Эту энергию можно также записать в виде

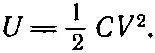
(8.10)

Вспоминая, что емкость проводящей сферы (по отношению к бесконечности) равна

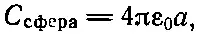
мы немедленно получим из уравнения (8.9) энергию заряженной сферы

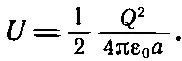(8.11)

Это выражение, конечно, относится также и к энергии тонкого сферического слоя с полным зарядом Q ; получается 5/ 6энергии однородно заряженного шара [уравнение (8.7)].

Посмотрим, как применяется понятие электростатической энергии. Рассмотрим два вопроса. Какова сила, действующая между обкладками конденсатора? Какой вращательный (крутящий) момент вокруг некоторой оси испытывает заряженный проводник в присутствии другого проводника с противоположным зарядом? На такие вопросы легко ответить, пользуясь нашим выражением (8.9) для электростатической энергии конденсатора и принципом виртуальной работы (см. вып. 1, гл. 4, 13 и 14).

Применим этот метод для определения силы, действующей между двумя обкладками плоского конденсатора. Если мы представим, что промежуток между пластинами расширился на небольшую величину Δz, то тогда механическая работа, производимая извне для того, чтобы раздвинуть обкладки, была бы равна

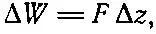(8.12)

где F — сила, действующая между обкладками. Эта работа обязана быть равной изменению электростатической энергии конденсатора, если только заряд конденсатора не изменился.

Согласно уравнению (8.9), энергия конденсатора первоначально была равна

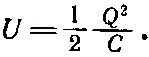
Изменение в энергии (если мы не допускаем изменения величины заряда) тогда равно

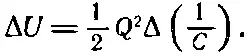(8.13)

Приравнивая (8.12) и (8.13), получаем

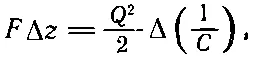(8.14)

что может также быть записано в виде

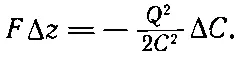(8.15)

Ясно, эта сила здесь возникает от притяжения зарядов на обкладках; мы видим, однако, что заботиться о том, как там они распределены, нам нечего; единственное, что нам нужно, — это учесть емкость С .

Легко понять, как обобщить эту идею на проводники произвольной формы и на прочие составляющие силы. Заменим в уравнении (8.14) F той составляющей, которая нас интересует, а Δz — малым смещением в соответствующем направлении. Или если у нас есть электрод, насаженный на какую-то ось, и мы хотим знать вращательный момент τ, то запишем виртуальную работу в виде

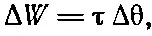
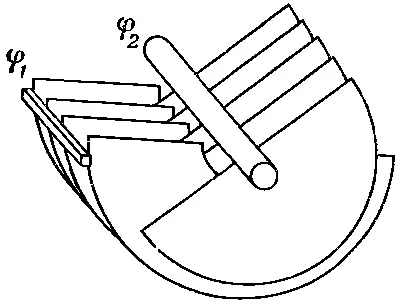
где Δθ — небольшой угловой поворот. Конечно, теперь Δ(1/C) должно быть изменением 1/ С , отвечающим повороту на Δθ. Таким способом мы можем определить вращательный момент, действующий на подвижные пластины переменного конденсатора, показанного на фиг. 8.3.