Ричард Фейнман - Том 2. Электромагнетизм и материя

Поля бывают также векторными. Идея их очень проста. В каждой точке пространства задается вектор. Он меняется от точки к точке. Рассмотрим в виде примера вращающееся тело. Скорость материала тела во всякой точке — это вектор, который является функцией ее положения (фиг. 2.2).

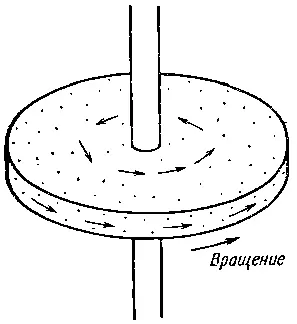
Фиг. 2.2. Скорости атомов во вращающемся теле — пример векторного поля.

Другой пример — поток тепла в бруске из некоторого материала. Если в одной части бруска температура выше, а в другой — ниже, то от горячей части к холодной будет идти поток тепла. Тепло в разных частях бруска будет растекаться в различных направлениях. Поток тепла — это величина, имеющая направление; обозначим ее h; длина этого вектора пусть измеряет количество протекающего тепла. Векторы потока тепла также изображены на фиг. 2.1.

Определим теперь hболее точно. Длина вектора потока тепла в данной точке — это количество тепловой энергии, проходящее за единицу времени и в пересчете на единицу площади сквозь бесконечно малый элемент поверхности, перпендикулярный к направлению потока. Вектор указывает направление потока (фиг. 2.3).

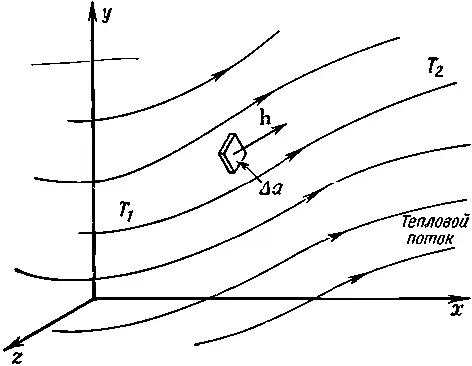
Фиг. 2.3. Тепловой поток — векторное поле. Вектор hуказывает направление потока. Абсолютная величина его выражает энергию, переносимую за единицу времени через элемент поверхности, ориентированный поперек потока, деленную на площадь элемента поверхности.

В буквенных обозначениях: если ΔJ — тепловая энергия, протекающая за единицу времени сквозь элемент поверхности Δа, то

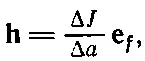(2.9)

где е f— единичный вектор направления потока Вектор hможно определить и иначе — через его компоненты. Зададим себе вопрос, сколько тепла протекает через малую поверхность под произвольным углом к направлению потока. На фиг. 2.4 мы изобразили малую поверхность Δa 2под некоторым углом к поверхности Δa t, которая перпендикулярна к потоку.

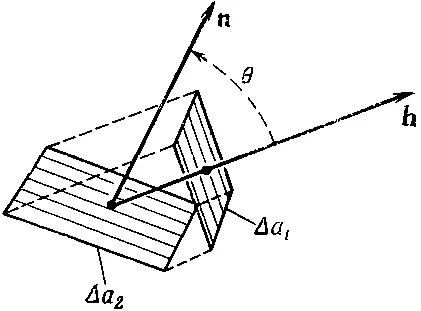
Фиг. 2.4. Тепловые потоки сквозь Aа 2 и сквозь Aa 1 одинаковы.

Единичный вектор nперпендикулярен к поверхности Δа 2. Угол θ между nи hравен углу между поверхностями (так как h— нормаль к Δa 1). Чему теперь равен поток тепла через Δа 2 на единицу площади ? Потоки сквозь Δа 2и Δа 1равны между собой, отличаются только площади. Действительно, Δа 1=Δа 2cosθ. Поток тепла через Δа 2равен

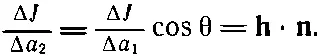(2.10)

Поясним это уравнение: поток тепла (в единицу времени и на единицу площади) через произвольный элемент поверхности с единичной нормалью nравен h· n. Можно еще сказать так: компонента потока тепла, перпендикулярная к элементу поверхности Δа 2, равна h· n. Можно, если мы хотим, считать эти утверждения определением h. Сходные идеи мы применим и к другим векторным полям.

Когда поля меняются со временем, то их изменение можно описать, задав их производные по t . Мы хотим также описать и их изменение в пространстве, потому что мы интересуемся связью, скажем, между температурой в некоторой точке и в точке с ней рядом. Как же задать производную температуры по координате? Дифференцировать температуру по х ? Или по у , или по z?

Осмысленные физические законы не зависят от ориентации системы координат. Поэтому их нужно писать так, чтобы по обе стороны знака равенства стояли скаляры или векторы. Что же такое производная скалярного поля, скажем, ∂ T /∂ x ? Скаляр ли это, или вектор, или еще что? Это, как легко понять, ни то ни другое, потому что если взять другую ось х , то ∂ T /∂ x изменится. Но заметьте: у нас есть три возможных производных: ∂ T /∂ x , ∂ T /∂ y и ∂ T /∂ z . Три сорта производных, а ведь мы знаем, что нужно как раз три числа, чтобы образовать вектор. Может быть, эти три производные и представляют собой компоненты вектора:

(2.11)

Ясно, конечно, что, вообще говоря, не из любых трех чисел можно составить вектор. О векторе можно говорить только тогда, когда при повороте системы координат компоненты преобразуются по правильному закону. Так что следует проследить, как меняются эти производные при повороте системы координат. Мы покажем, что (2.11) — действительно вектор. Производные действительно преобразуются при вращении системы координат так, как полагается.

В этом можно убедиться по-разному. Можно, например, задать себе вопрос, ответ на который не должен зависеть от системы координат, и попытаться выразить ответ в «инвариантной» форме. К примеру, если S= A· Bи если Аи В— векторы, то мы знаем (это доказано в вып. 1, гл. 11), что S — скаляр. Мы знаем , что S — скаляр, не проверяя, меняется ли он при изменении системы координат. Ему ничего иного не остается , раз он является скалярным произведением двух векторов. Подобным же образом, если мы знаем , что А— вектор, и у нас есть три числа B 1, B 2, В 3, и мы обнаруживаем, что

(2.12)

(где S в любой системе координат одно и то же), то три числа B 1, B 2, В 3обязаны быть компонентами В х, В у, В zнекоторого вектора В.

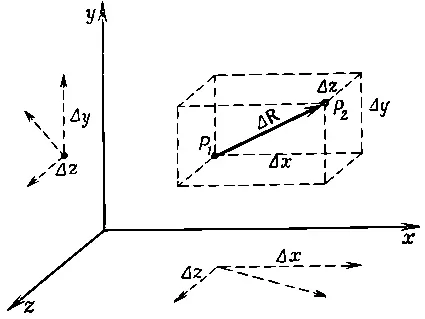
Рассмотрим теперь температурное поле. Возьмем две точки P 1и Р 2, разделенные маленьким расстоянием Δ R.Температура в Р 1есть T 1, а в Р 2она равна T 2, и их разница ΔТ=Т 2-Т 1.Температура в этих реальных физических точках, конечно, не зависит от того, какие оси мы выбрали для измерения координат. В частности, ΔT — тоже число, не зависящее от системы координат. Это скаляр.

Выбрав удобную систему координат, мы можем написать

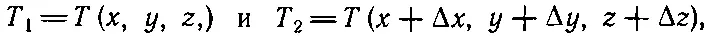
где Δx, Δy, Δz — компоненты вектора Δ R(фиг. 2.5).