Ричард Фейнман - Том 2. Электромагнетизм и материя

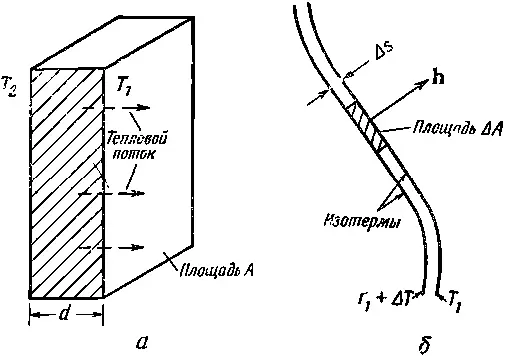
Фиг. 2.7. Тепловой поток через плиту (а) и бесконечно малая плитка, параллельная изотермической поверхности в большом блоке вещества (б).

Обозначая через J тепловую энергию, проходящую сквозь плиту за единицу времени, мы напишем

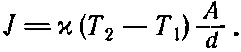(2.42)

Коэффициент пропорциональности ϰ (каппа) называется теплопроводностью .

Что произойдет в более сложных случаях, скажем, в блоке материала необычной формы, в котором температура как-то прихотливо меняется? Рассмотрим тонкий слой материала и представим себе плиту наподобие изображенной на фиг. 2.7, а, но в миниатюре. Ориентируем ее торцы параллельно изотермическим поверхностям (фиг. 2.7, б), так что для этой малой плиты выполняется уравнение (2.42).

Если площадь этой плиты ΔА, то поток тепла за единицу времени равен

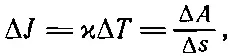(2.43)

где Δs — толщина плиты. Но Δ J /ΔA мы раньше определили как абсолютную величину h— вектора, направленного туда, куда течет тепло. Тепло течет от T 1+ΔT к T 1, так что вектор hперпендикулярен изотермам (фиг. 2.7, б ). Далее, ΔТ/Δs как раз равно быстроте изменения Т с изменением положения. А поскольку изменения положения перпендикулярны изотермам, то наше ΔT/Δs — это максимальная скорость изменения. Она равна поэтому величине ∇ Т . И, наконец, раз направления ∇ Т и h противоположны, то (2.43) можно записать в виде векторного уравнения

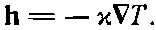(2.44)

(Знак минус написан потому, что тепло течет в сторону понижения температуры.) Уравнение (2.44) — это дифференциальное уравнение теплопроводности в массиве вещества. Вы видите, что это чисто векторное уравнение. С обеих сторон стоят векторы (если ϰ число). Это обобщение на произвольный случай частного соотношения (2.42), верного для прямоугольной плиты.

Мы с вами должны будем научиться выписывать все соотношения элементарной физики [наподобие (2.42)] в этих хитроумных векторных обозначениях. Они полезны не только потому, что уравнения начинают от этого выглядеть проще. В них намного яснее проступает физическое содержание уравнений безотносительно к выбору системы координат.

Пока мы имели дело только с первыми производными. А почему не со вторыми? Из вторых производных можно составить несколько комбинаций:

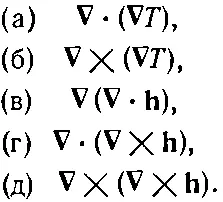(2.45)

Вы можете убедиться, что никаких иных комбинаций быть не может.

Посмотрим сперва на вторую комбинацию (б). Она имеет ту же форму, что и

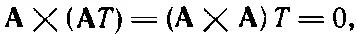
потому что А× Авсегда нуль. Значит,

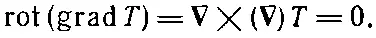(2.46)

Можно понять, как это получается, если расписать одну из компонент:

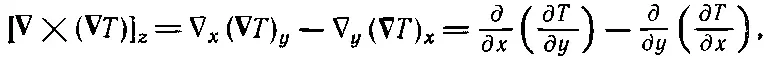(2.47)

что равно нулю [по уравнению (2.8)]. Это же верно и для других компонент. Стало быть, ∇×( ∇T)=0 для любого распределения температур, да и для всякой скалярной функции.

Возьмем второй пример. Посмотрим, нельзя ли получить нуль другим путем. Скалярное произведение вектора на векторное произведение, содержащее этот вектор, равно нулю

(2.48)

потому что А× Вперпендикулярно к Аи не имеет тем самым составляющих вдоль А. Сходная комбинация стоит в списке (2.45) под номером (г):

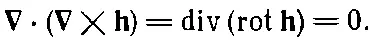(2.49)

В справедливости этого равенства опять-таки легко убедиться, проделав выкладки на компонентах.

Теперь сформулируем без доказательства две теоремы. Они очень интересны и весьма полезны для физиков.

В физических задачах часто оказывается, что ротор какой-то величины (скажем, векторного поля А) равен нулю. Мы видели в уравнении (2.46), что ротор градиента равен нулю. (Это легко запоминается по свойствам векторов.) Далее, может оказаться, что Абудет градиентом какой-то величины, потому что тогда ротор Ас необходимостью обратится в нуль. Имеется интересная теорема, утверждающая, что если ротор Аесть нуль, то тогда А непременно окажется чьим - то градиентом; существует некоторое скалярное поле ψ (пси), такое, что A=gradψ. Иными словами, справедлива

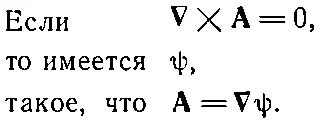(2.50)

Сходная теорема формулируется и для случая, когда дивергенция Аесть нуль. Из уравнения (2.49) видно, что дивергенция ротора любой величины равна всегда нулю. Если вам случайно встретилось векторное поле D, для которого div D— нуль, то вы имеете право заключить, что Dэто ротор некоторого векторного поля С.

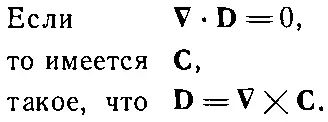(2.51)

Перебирая всевозможные сочетания двух операторов ∇, мы обнаружили, что два из них всегда дают нуль. Займемся теперь теми, которые не равны нулю. Возьмем комбинацию ∇·( ∇T), первую в нашем списке. В общем случае это не нуль. Выпишем компоненты

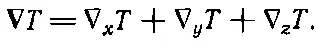
Далее,

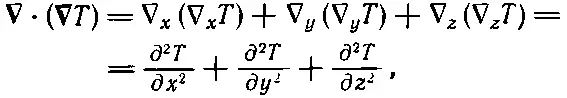(2.52)

что может, вообще говоря, быть любым числом. Это скалярное поле.

Вы видите, что скобок можно не ставить, а вместо этого писать, не рискуя ошибиться:

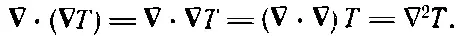(2.53)

Можно рассматривать ∇ 2как новый оператор. Это скалярный оператор. Так как он в физике встречается часто, ему дали особое имя — лапласиан .