Ричард Фейнман - Том 2. Электромагнетизм и материя

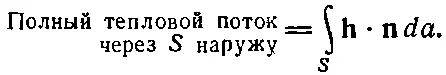(3.11)

Этот интеграл мы будем называть «поток hчерез поверхность». Мы рассматриваем hкак «плотность потока» тепла, а поверхностный интеграл от h— это общий поток тепла наружу через поверхность, т. е. тепловая энергия за единицу времени (джоули в секунду).

Мы хотим эту идею обобщить на случай, когда вектор не представляет собой потока какой-то величины, а, скажем, является электрическим полем. Конечно, если это будет нужно, то и в этом случае все равно можно проинтегрировать нормальную составляющую электрического поля по площади. Хотя теперь она уже не будет ничьим потоком, мы все еще будем употреблять слово «поток». Мы будем говорить, что

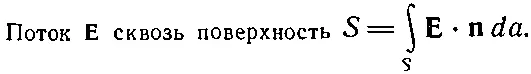(3.12)

Слову «поток» мы придаем смысл «поверхностного интеграла от нормальной составляющей» некоторого вектора. То же определение будет применяться и тогда, когда поверхность незамкнута.

А возвращаясь к частному случаю потока тепла, обратим внимание на те случаи, когда количество тепла сохраняется . Представьте себе, к примеру, материал, в котором после первоначального подогрева не происходит ни дальнейшего подвода, ни поглощения тепла. Тогда, если из какой-то замкнутой поверхности наружу поступает тепло, содержание тепла во внутреннем объеме должно падать. Так что в условиях, когда количество тепла сохраняется, мы говорим, что

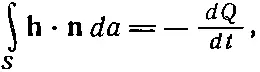(3.13)

где Q — запас тепла внутри S . Поток тепла из S наружу равен со знаком минус быстроте изменения со временем общего запаса тепла Q внутри S . Это толкование возможно оттого, что речь идет о потоке тепла, и оттого, что мы предположили, что количество тепла сохраняется. Конечно, если бы внутри объема создавалось тепло, нельзя было бы говорить о полном запасе тепла в нем.

Укажем теперь на интересное свойство потока любого вектора. Можете при этом представлять себе вектор потока тепла, но верно это будет и для произвольного векторного поля С. Представьте себе замкнутую поверхность S , окружающую объем V . Разобьем теперь объем на две части каким-то «сечением» (фиг. 3.4). Получились два объема и две замкнутые поверхности. Объем V 1окружен поверхностью S 1, составленной частью из прежней поверхности S aи частью из «сечения» S ab. Объем V 2окружен поверхностью S 2, составленной из остатка прежней поверхности (S b) и замкнутой сечением S ab. Зададим вопрос: если мы рассчитаем поток через поверхность S 1и прибавим к нему поток сквозь поверхность S 2, будет ли их сумма равна потоку через первоначальную поверхность? Ответ гласит: «Да». Потоки через часть S ab, общую обеим поверхностям S 1и S 2, в точности сократятся. Для потока вектора Сиз V 1можно написать

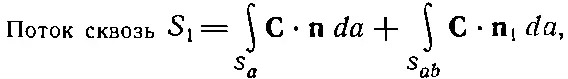(3.14)

а для потока из V 2:

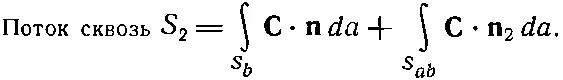(3.15)

Заметьте, что во втором интеграле мы обозначили внешнюю нормаль к S abбуквой n 1, если она относится к S 1, и буквой n 2, если она относится к S 2(см. фиг. 3.4).

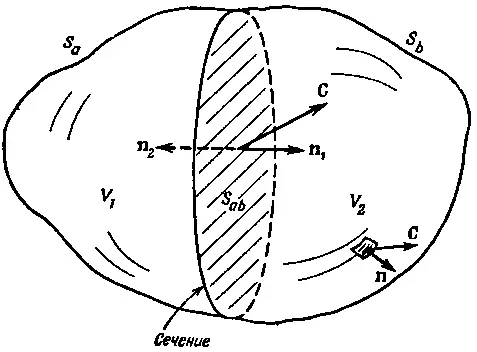
Фиг. 3.4. Объем V, заключенный внутри поверхности S, делится на две части «сечением» (поверхностью S ab ). Получается объем V 1 , окруженный поверхностью S 1 =S a +S ab , и объем V 2 , окруженный поверхностью S 2 =S b +S ab .

Ясно, что n 1=-n 2, и тем самым

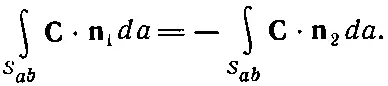(3.16)

Складывая теперь уравнения (3.14) и (3.15), мы убеждаемся, что сумма потоков сквозь S 1и S 2как раз равна сумме двух интегралов, которые, взятые вместе, дают поток через первоначальную поверхность S = S a + S b .

Мы видим, что поток через всю внешнюю поверхность S можно рассматривать как сумму потоков из тех двух частей, на которые разрезан объем. Эти части можно еще разрезать: скажем, V 1разбить пополам. Опять придется прибегнуть к тем же доводам. Так что для любого способа разбиения первоначального объема всегда остается справедливым то свойство, что поток через внешнюю поверхность (первоначальный интеграл) равен сумме потоков изо всех внутренних частей.

Рассмотрим теперь частный случай потока из маленького кубика [6] Конечно, последующие выкладки в равной мере относятся и к любому прямоугольному параллелепипеду. и получим интересную формулу. Ребра куба пусть направлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у , z, ребро куба в направлении х равно Δx, ребро куба (а точнее, бруска) в направлении у равно Δy, а в направлении z равно Δz. Мы хотим найти поток векторного поля Счерез поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5).

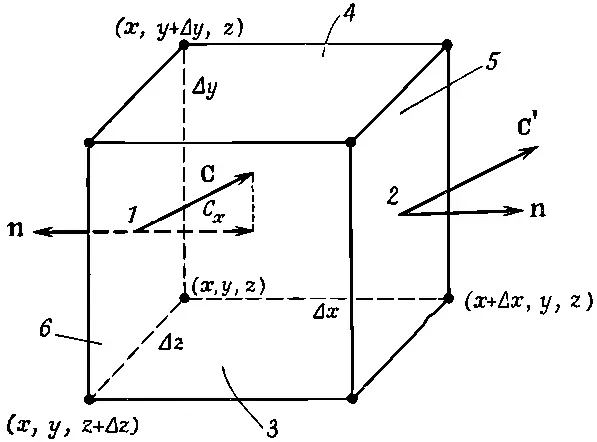
Фиг. 3.5. Вычисление потока вектора С из маленького кубика.

Поток наружу сквозь нее равен x-компоненте Сс минусом, проинтегрированной по площади грани. Он равен

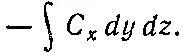
Так как куб считается малым, этот интеграл можно заменить значением С хв центре грани 1эту точку мы обозначили (1), умноженным на площадь грани ΔyΔz:

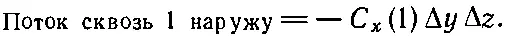
Подобным же образом поток наружу через грань 2 равен

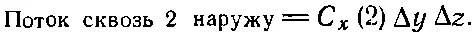
Величины C x (1) и С х (2), вообще говоря, слегка отличаются. Если Δх достаточно мало, то можно написать

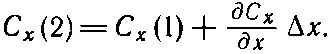
Существуют, конечно, и другие члены, но в них входит (Δx) 2и высшие степени Δx, и в пределе малых Δx ими запросто можно пренебречь. Значит, поток сквозь грань 2 равен