Ричард Фейнман - Том 2. Электромагнетизм и материя

Контур Γ 1состоит из Γ a— части первоначальной кривой слева от (1) и (2) и «соединения» Γ ab . Контур Γ 2состоит из остатка первоначальной кривой плюс то же соединение.

Циркуляция вдоль Γ 1есть сумма интеграла вдоль Γ аи вдоль Γ аЬ. Точно так же и циркуляция вдоль Γ 2есть сумма двух частей, одной вдоль Γ b, другой — вдоль Г ab. Интеграл вдоль Г abдля кривой Γ 2имеет знак, противоположный тому знаку, который он имел для кривой Γ 1, потому что направления обхода противоположны (в обоих криволинейных интегралах направления поворота нужно брать одни и те же).

Повторяя прежние аргументы, мы можем убедиться, что сумма двух циркуляции даст как раз криволинейный интеграл вдоль первоначальной кривой Γ. Интегралы по Γ abсократятся. Циркуляция по одной части плюс циркуляция вдоль другой равняется циркуляции вдоль внешней линии. Этот процесс разрезания большого контура на меньшие можно продолжить. При сложении циркуляции по меньшим контурам смежные части будут сокращаться, так что сумма их сведется к циркуляции вдоль единственного первоначального контура.

Теперь предположим, что первоначальный контур — это граница некоторой поверхности. Существует бесконечное множество поверхностей, границей которых служит все тот же первоначальный замкнутый контур. Наши результаты не зависят, однако, от выбора этих поверхностей. Сперва мы разобьем наш первоначальный контур на множество малых контуров, лежащих на выбранной поверхности (фиг. 3.9).

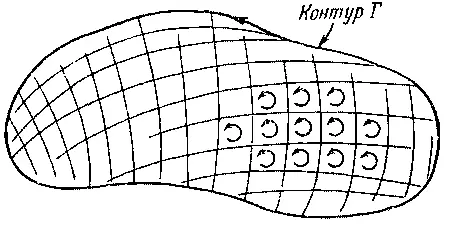
Фиг. 3.9. Некоторая поверхность, ограниченная контуром Γ. Поверхность разделена на множество маленьких участков, каждый примерно в форме квадрата. Циркуляция по Γ есть сумма циркуляции по всем маленьким контурам.

Какой бы ни была форма поверхности, но если малые контуры сделать достаточно малыми, всегда можно будет считать каждый из них замыкающим достаточно плоскую поверхность. Кроме того, каждый из них можно сделать очень похожим на квадрат. И циркуляцию вокруг большого контура Γ можно найти, подсчитав циркуляции по всем квадратикам и сложив их.

Как нам найти циркуляцию по каждому квадратику? Все зависит от того, как квадрат ориентирован в пространстве. Если ориентация его подобрана удачно (к примеру, он расположен в одной из координатных плоскостей), то расчет сделать легко. Так как пока мы не делали никаких предположений об ориентации осей координат, мы вправе выбрать их так, чтобы тот квадратик, на котором мы сосредоточили свое внимание, оказался в плоскости ху (фиг. 3.10).

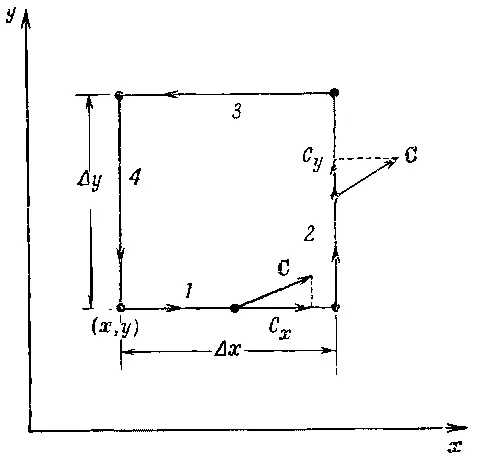
Фиг. 3.10. Вычисление циркуляции вектора С по маленькому квадратику.

Если результат расчета будет выражен в векторной записи, то можно говорить, что он не зависит от специальной ориентации плоскости.

Мы хотим теперь найти циркуляцию поля Спо нашему квадратику. Криволинейное интегрирование легко проделать, если квадратик сделать таким маленьким, чтобы вектор Сна протяжении одной стороны квадрата менялся очень мало. (Это предположение выполняется тем лучше, чем меньше квадратик, так что на самом деле речь идет о бесконечно малых квадратиках.) Отправившись от точки ( х, у ) — в левом нижнем углу фигуры,— мы обойдем весь квадрат в направлении, указанном стрелками. Вдоль первой стороны, отмеченной цифрой 1, касательная составляющая равна С х (1), а расстояние равно Δх. Первая часть интеграла равна C x(1) Δх. Вдоль второй стороны получится С у(2) Δy. Вдоль третьей мы получим -С x(3) Δх, а вдоль четвертой -C y(4) Δy. Знаки минус стоят потому, что нас интересует касательная составляющая в направлении обхода. Весь криволинейный интеграл тогда равен

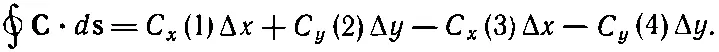(3.31)

Посмотрим теперь на первый и третий члены. В сумме они дают

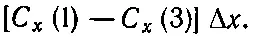(3.32)

Вам может показаться, что в принятом приближении эта разность равна нулю. Но это только в первом приближении. Мы можем быть более точными и учесть скорость изменения С х , тогда можно написать

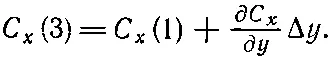(3.33)

В следующем приближении пойдут члены с (Δy) 2, но ввиду того, что нас интересует в конечном счете только предел при Δy→0, то этими членами можно пренебречь. Подставляя (3.33) в (3.32), мы получаем

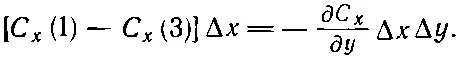(3.34)

Производную при нашей точности можно брать в точке ( х, у ). Подобным же образом оставшиеся два члена можно написать в виде

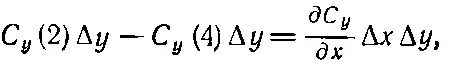(3.35)

и циркуляция по квадрату тогда равна

(3.36)

Интересно, что в скобках получилась как раз z-компонента ротора С . Множитель ΔxΔy— это площадь нашего квадрата. Так что циркуляцию (3.36) можно записать как

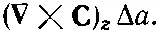
Но z-компонента это на самом деле компонента, нормальная к элементу поверхности. Поэтому циркуляцию вокруг квадратика можно задать и в инвариантной векторной записи:

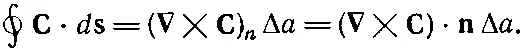(3.37)

В результате имеем: циркуляция произвольного вектора Спо бесконечно малому квадрату равна произведению составляющей ротора С, нормальной к поверхности, на площадь квадрата.

Циркуляция по произвольному контуру Γ легко теперь может быть увязана с ротором векторного поля. Натянем на контур любую подходящую поверхность S (как на фиг. 3.11) и сложим между собой циркуляции по всем бесконечно малым квадратикам на этой поверхности.

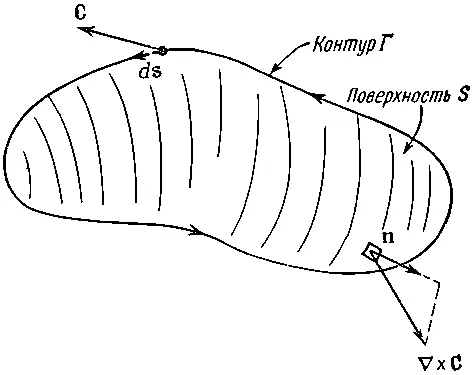
Фиг. 3.11. Циркуляция вектора С по Γ равна поверхностному интегралу от нормальной компоненты вектора ∇×С.

Сумма может быть записана в виде интеграла. В итоге получится очень полезная теорема, называемая теоремой Стокса [по имени физика Стокса].