Ричард Фейнман - Том 2. Электромагнетизм и материя

Однако настоящая глава, хоть она и посвящена электростатике, не будет касаться самых красивых и тонких вопросов этой науки. В ней будут рассмотрены лишь такие ситуации, в которых можно предположить, что расположение всех зарядов известно. Но и в этом случае, прежде чем научиться справляться со сложными случаями, естественно сначала освоиться с простыми.

Логично было бы принять за отправную точку уравнения (4.5) и (4.6). Но легче начать с другого, а потом вернуться к этим уравнениям. Результат получится одинаковый. Мы начнем с закона, о котором говорилось раньше,— с закона Кулона, утверждающего, что между двумя покоящимися зарядами действует сила, прямо пропорциональная произведению зарядов и обратно пропорциональная квадрату расстояния между ними. Сила направлена по прямой от одного заряда к другому.

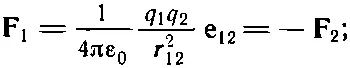(4.9)

здесь F 1— сила, действующая на заряд q 1; е 12— единичный вектор, направленный от q 2к q 1, а r 12— расстояние между q 1и q 2. Сила F 2, действующая на q 2, равна и противоположна силе F 1. Множитель пропорциональности по историческим причинам пишется в виде 1/ 4πе 0. В системе единиц СИ, которой мы пользуемся, он определяется как 10 -7от квадрата скорости света. Так как скорость света примерно 3·10 8 м / сек , то множитель приблизительно равен 9·10 9, и единица оказывается равной ньютон · м 2/ кулон 2, или вольт · м / кулон

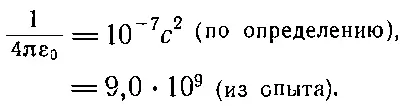(4.10)

Если зарядов больше двух (а именно такие случаи наиболее интересны), то закон Кулона нужно дополнить другим существующим в природе фактом: сила, действующая на заряд, есть векторная сумма кулоновских сил, действующих со стороны всех прочих зарядов. Этот экспериментальный факт называется «принципом наложения», или «принципом суперпозиции». Это и есть все, что имеется в электростатике. Если добавить к закону Кулона принцип наложения, то больше ничего в ней не останется. Точно к таким же выводам, ни больше, ни меньше, приведут уравнения электростатики, уравнения (4.5) и (4.6).

Применяя закон Кулона, удобно ввести понятие об электрическом поле. Мы говорим, что поле F(1) — это сила, действующая со стороны прочих зарядов на единицу заряда q 1. Деля (4.9) на q 1, мы получаем для действия всех зарядов, кроме q 1

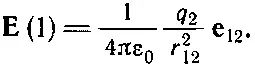(4.11)

Кроме того, мы считаем, что Е(1) описывает нечто, существующее в точке (1), даже если в ней нет заряда q 1(в предположении, что все прочие заряды сохранили свои позиции). Мы говорим: Е(1) — это электрическое поле в точке (1).

Электрическое поле Е— это вектор, так что в (4.11) на самом деле написаны три уравнения, по одному для каждой компоненты. Расписывая x -компоненту в явном виде, получаем

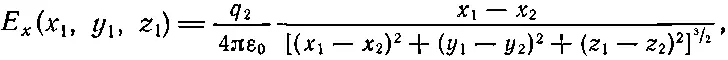(4.12)

и точно так же для остальных компонент.

Если зарядов много, то поле Ев любой точке (1) равно сумме вкладов от всех зарядов. Каждый член в сумме будет выглядеть как (4.11) или (4.12). Пусть q j — величина j-го заряда, а r 1 j — смещение q j от точки (1); тогда мы напишем

(4.13)

что означает, конечно,

(4.14)

и т. д.

Часто бывает удобно игнорировать тот факт, что заряды всегда существуют в виде отдельных кусочков, таких, как электроны или протоны, а считать, что они размазаны сплошным пятном, или, как говорят, описываются «распределением». До тех пор пока нам все равно, что происходит в малых масштабах, такое описание вполне законно. Распределение заряда описывается «плотностью заряда» ρ ( х, у, z ). Если количество заряда в небольшом объеме ΔV 2близ точки (2) есть Δq 2, то ρ определяется равенством

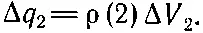(4.15)

Пользуясь теперь законом Кулона при непрерывном распределении заряда, мы заменяем в уравнениях (4.13) или (4.14) суммы интегралами по всему объему, содержащему заряды. Получается

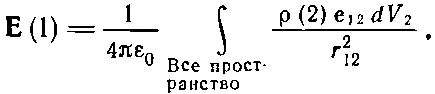(4.16)

Некоторые предпочитают писать

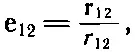
где r 12— вектор смещения от (2) к (1) (фиг. 4.1).

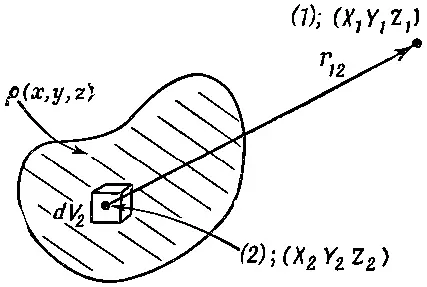
Фиг. 4.1. В точке (1) электрическое поле Е от некоторого распределения зарядов получается из интеграла по распределению. Точка (I) может находится также внутри распределения.

Интеграл для Етогда запишется в виде

(4.17)

Если мы хотим действительно провести интегрирование до конца, то обычно приходится интегралы расписывать подробнее. Для x-компоненты уравнений (4.16) или (4.17) получается

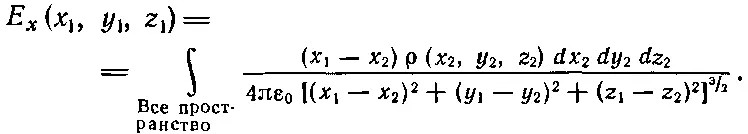(4.18)

Мы не собираемся вычислять что-либо по этой формуле. Написали мы ее здесь только для того, чтобы подчеркнуть, что мы полностью решили те электростатические задачи, в которых известно расположение всех зарядов.

Дано : Заряды.

Определить : Поля.

Решение : Возьми этот интеграл.

Так что по существу все сделано; остается только проделать сложные интегрирования по трем переменным. Эта работа в самый раз для счетной машины!

Пользуясь этими интегралами, мы можем найти поле заряженной плоскости, заряженной линии, заряженной сферы и любого выбранного распределения. Хотя мы сейчас начнем чертить силовые линии, говорить о потенциалах и вычислять дивергенции, важно понимать, что ответ на все решаемые задачи в принципе уже готов. Просто порой бывает легче взять интеграл, придумав фокус, чем проделывать все выкладки честно. Но чтобы догадываться, нужно научиться разным ухищрениям. Быть может, лучше было бы вычислять интегралы непосредственно, а не тратить силы на остроумные способы решения да демонстрировать свою сообразительность. Но все-таки мы пойдем по пути развития сообразительности. Переходим, таким образом, к обсуждению некоторых других особенностей электрического поля.