Ричард Фейнман - Том 3. Квантовая механика

Если вас тревожит, что такого рода рассуждения могут в квантовой механике оказаться неправильными, стоит потратить минутку, чтобы показать, что и по квантовой механике все обстоит так же. Начальное (дораспадное) состояние, которое мы обозначим |Λ 0, спин по +z>, обладает тем свойством, что если его повернуть вокруг оси z на угол φ, то вектор состояния умножается на фазовый множитель e i φ/2. (В повернутой системе вектор состояния равен e itf/2|Λ 0, спин но +z>.) Именно это и имеют в виду, говоря о спине вверх у частицы со спином 1/ 2. Поскольку поведение природы не зависит от нашего выбора осей, то конечное состояние системы «протон плюс пион» должно обладать тем же свойством. Конечное состояние мы можем, например, записать в виде

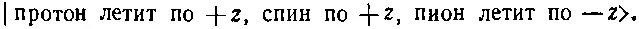
Но движение пиона на самом деле не нужно оговаривать, потому что в выбранной нами системе пион всегда движется противоположно протону; наше описание конечного состояния можно упростить до

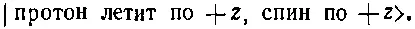
Так что же случится с этим состоянием, если мы повернем систему координат вокруг оси z на угол φ?

Раз протон и пион движутся вдоль оси z , их движение поворотом не изменишь. (Вот почему мы и выбрали этот частный случай; иначе бы наше рассуждение не прошло.) Значит, с пионом ничего не случится, потому что спин его равен нулю. У протона, однако, спин равен 1/ 2. Если его спин направлен вверх, он в ответ на поворот изменит фазовый множитель в e iφ/2раз. (А если бы спин его был направлен вниз, то изменение фазы стало бы e -iφ/2.) Но если момент количества движения обязан сохраняться (а это так, ибо в гамильтониане нет факторов, зависящих от внешних воздействий), то изменение фазы из-за поворота должно быть до распада и после распада одно и то же. Итак, единственная возможность состоит в том, что спин протона будет направлен вверх. Если протон двинулся вверх, то и спин его должен быть направлен вверх.

Мы, следовательно, заключаем, что сохранение момента количества движения разрешает процесс, показанный на фиг. 15.7, б , но не разрешает процесса, показанного на фиг. 15.7, в . А раз мы знаем, что распад все же происходит, то, значит, имеется некоторая амплитуда для процесса, показанного на фиг. 15.7, б , когда протон летит вверх и спин его при этом тоже смотрит вверх. И мы обозначим буквой а амплитуду того, что в бесконечно малый промежуток времени произойдет такой распад [67] Мы сейчас предполагаем, что механизм квантовой механики вам настолько знаком, что обо всем можно говорить на чисто физическом языке, не тратя времени на расписывание всех математических деталей. Но если то, что мы здесь говорим, вам не очень ясно, то обратитесь к концу этого параграфа, где приведены некоторые недостающие детали. .

Теперь посмотрим, что было бы, если бы спин Λ 0вначале был направлен вниз. Опять рассматриваем распады, в которых протон взлетает вверх по оси z, как показано на фиг. 15.8.

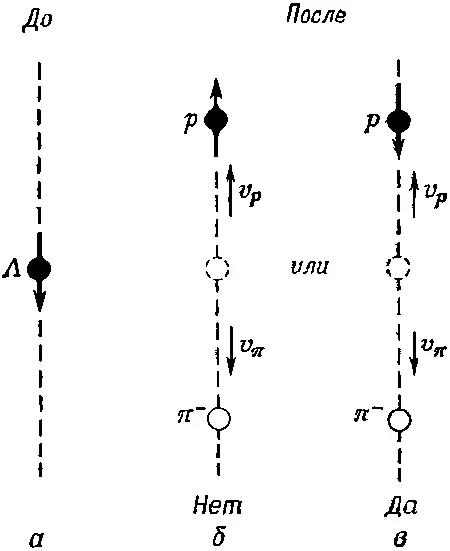
Фиг. 15.8. Распад вдоль оси z для Λ 0 со спином, направленным вниз.

Вам, конечно, теперь ясно, что в этом случае спин протона направлен вниз (если только момент количества движения сохраняется). Обозначим амплитуду такого распада буквой b .

Об амплитудах а и b мы ничего больше сказать не сможем. Они зависят от внутренней механики частицы Λ 0и от слабых распадов, и никто пока не знает, как их подсчитывать. Их приходится получать из опыта. Но, зная только эти две амплитуды, мы можем узнать об угловом распределении распадов все, что захотим. Надо только всегда тщательно и полностью определять те состояния, о которых идет речь.

Мы хотим знать вероятность того, что протон вылетит под углом θ к оси z (в некоторый узкий телесный угол ΔΩ), как показано на фиг. 15.6. Проведем новую ось z в этом направлении и обозначим ее z'! Как анализировать, что происходит вдоль этой оси, мы знаем. По отношению к ней спин Λ 0уже не направлен вверх, а имеет какую-то амплитуду того, что он окажется направленным вверх и какую-то — вниз. Все это мы уже подсчитывали в гл. 4, а потом опять в гл. 8 [уравнение (8.30)] (вып. 8). Амплитуда того, что спин будет направлен вверх, есть cosθ/2, а амплитуда того, что спин будет смотреть вниз, есть -sinθ/2 [68] Мы провели ось z ' в плоскости xz и используем матричные элементы для R y (θ). То же получилось бы и при другом выборе осей. . Когда спин Λ 0направлен вверх по оси z', она испустит протон в направлении z с амплитудой а . Значит, амплитуда того, что по направлению z пройдет протон, держа свой спин вверх, равна

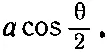(15.33)

Точно так же амплитуда того, что вдоль положительной оси z пройдет протон, направив свой спин вниз, равна

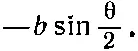(15.34)

Те два процесса, к которым относятся эти амплитуды, показаны на фиг. 15.9.

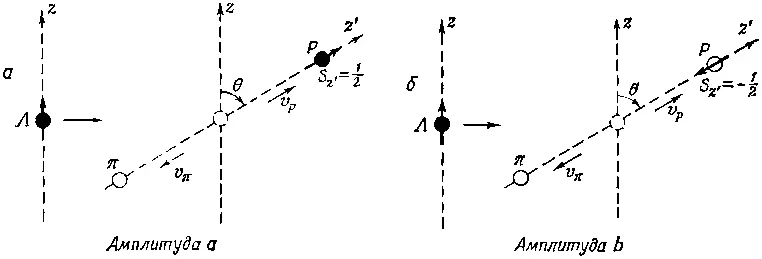
Фиг. 15.9. Два возможных состояния распада Λ 0 .

Теперь зададим такой немудреный вопрос. Пусть мы собираемся регистрировать протоны, вылетающие под углом θ, не интересуясь их спином. Два спиновых состояния (вверх и вниз по оси z') различимы, даже если бы мы того и не хотели. Значит, чтобы получить вероятность, надо амплитуды возвысить в квадрат и сложить. Вероятность f (θ) обнаружить протон в небольшом телесном угле ΔΩ при θ равна

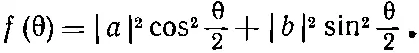(15.35)

Вспоминая, что sin 2θ/2= 1/ 2(1-cosθ) и cos 2θ/2= 1/ 2(1+cosθ), запишем f (θ) так:

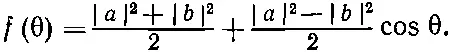(15.36)

Угловое распределение имеет вид

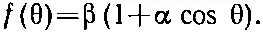(15.37)

Одна часть вероятности не зависит от θ, а другая зависит от cosθ линейно. Из измерений углового распределения мы можем получить α и β, а значит, и | а |, и | b |.

Можно получить ответ и на многие другие вопросы. Может быть, вас интересуют лишь те протоны, спин которых направлен вверх относительно старой оси z? Каждый член в (15.33) и (15.34) даст амплитуду того, что спин протона окажется направленным вверх или вниз по отношению к оси z '(|+ z '> и |- z '>). А состояние, когда спин направлен вверх относительно старой оси, |+z>, можно выразить через два базисных состояния |+ z '> и |-z'>. Можно тогда взять две амплитуды (15.33) и (15.34) с надлежащими коэффициентами (cosθ/2 и -sinθ/2) и получить полную амплитуду