Ричард Фейнман - Том 3. Квантовая механика

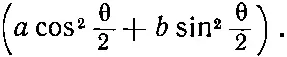
Ее квадрат даст вероятность того, что протон вылетит под углом θ со спином, направленным туда же, куда направлен спин Λ 0(вверх по оси z ).

Если бы четность сохранялась, можно было бы сделать еще одно утверждение. Распад на фиг. 15.8 — это просто зеркальное отражение, скажем в плоскости yz , распада с фиг. 15.7 [69] Вспомните, что спин — это аксиальный вектор и при отражении он переворачивается. . Если бы четность сохранялась, b равнялось бы либо a , либо - а . Тогда коэффициента в (15.37) был бы равен нулю и распад одинаково часто происходил бы во всех направлениях.

Результаты опытов говорят, однако, что при распаде асимметрия существует . Измеренное угловое распределение действительно, как мы предсказали, меняется по закону cosθ, а не по закону cos 2θ или по другой степени. Из этого углового распределения, стало быть, следует, что спин Λ 0равен 1/ 2. Кроме того, мы видим, что четность не сохраняется. Действительно, коэффициент a на опыте найден равным -0,62±0,05, так что b примерно вдвое больше а . Отсутствие симметрии относительно отражений совершенно очевидно.

Вы видите, как много можно вывести из сохранения момента количества движения. Еще некоторые примеры будут приведены в следующей главе.

Замечание после лекции . Под амплитудой а здесь мы подразумевали амплитуду того, что состояние |протон летит по +z, спин по +z> образовано за бесконечно малое время dt из состояния |Λ, спин по +z>, или, иными словами, что

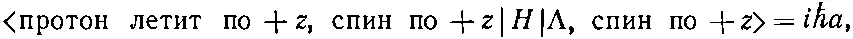(15.38)

где H — гамильтониан всего мира или по крайней мере той его части, которая ответственна за Λ-распад. Сохранение момента количества движения означает, что у гамильтониана должно быть такое свойство:

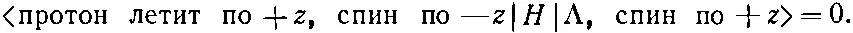(15.39)

Под амплитудой b подразумевается, что

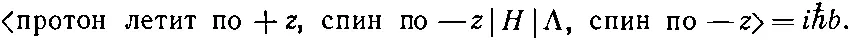(15.40)

Сохранение момента количества движения предполагает, что

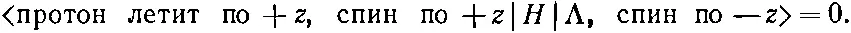(15.41)

Если вам не ясно, как написаны амплитуды (15.33) и (15.34), можно их записать в более математической форме. Когда мы писали (15.33), нам нужна была амплитуда того, что Λ со спином, направленным по +z, распадается на протон, движущийся вдоль направления + z ' и обладающий спином, направленным тоже по + z ', т. е.

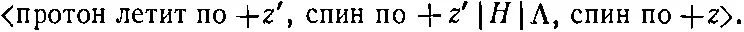(15.42)

По общим теоремам квантовой механики эту амплитуду можно записать так:

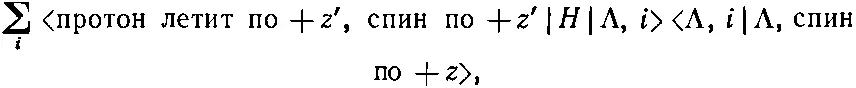(15.43)

где суммирование проводится но базисным состояниям |Λ, i > покоящейся Λ-частицы. Поскольку спин Λ-частицы равен 1/ 2, таких состояний два, в каком бы базисе мы ни работали. Если в качестве базисных мы выберем состояния со спином, направленным вверх и вниз по отношению к оси z'(|+z'>, |-z'>), то амплитуда (15.43) будет равна сумме

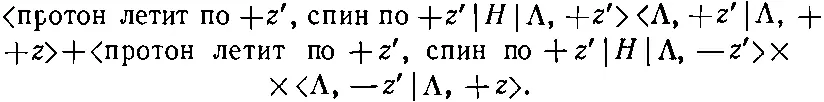(15.44).

Первый множитель в первом слагаемом равен а [из (15.38)], а первый множитель во втором слагаемом равен нулю — из формулы (15.41), в свою очередь следующей из сохранения момента количества движения. Второй множитель <���Λ, +z'|Λ, +z> из первого слагаемого — это как раз амплитуда того, что частица со спином 1/ 2, направленным вверх по одной оси, будет также обладать спином, направленным вверх по другой оси, повернутой относительно первой на угол θ. Такая амплитуда равна cosθ/2 [см. табл. 4.2 (вып. 8)]. Так что (15.44) равно просто а cos θ/2, как и было написано в (15.33). Амплитуда (15.34) следует из таких же рассуждений для Λ-частицы со спином, направленным вниз.

Теперь мы хотим собрать воедино все, что мы узнали о поворотах частиц со спином 1/ 2и спином 1; это будет удобно для дальнейшего. Ниже вы найдете таблицы двух матриц поворота R z (φ) и R y (θ) для частиц со спином 1/ 2, для частиц со спином 1 и для фотонов (частиц со спином 1 и нулевой массой).

Таблица 15.1. МАТРИЦЫ ПОВОРОТА ДЛЯ СПИНА ½. Два состояния :

|+>, вверх по оси z, m =+ 1 / 2

|—>, вниз по оси z, m =—1/2

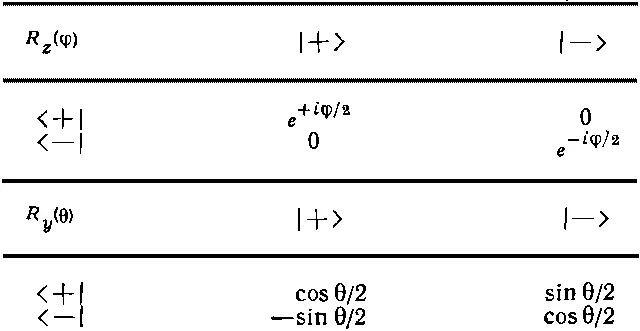
Таблица 15.2. МАТРИЦЫ ПОВОРОТА ДЛЯ СПИНА 1. Три состояния :

|+>, m =+1

| 0 >, m = 0

|—>, m =— 1

Таблица 15.3. ФОТОНЫ. Два состояния :

| R >= 1 /√ 2 (| x >+ iy >), m =+ 1 ( правополяризованные )

\ L >= 1 /√ 2 (\ x >— i | y >), m =— 1 ( левополяризованные )

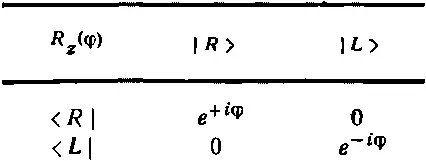
Для каждого из них приведены элементы матрицы < j | R | i > поворотов вокруг оси z или оси y . Они, конечно, в точности эквивалентны амплитудам типа <+ T |0 S >, которыми мы пользовались в предыдущих главах. Под R z (φ) мы понимаем, что берется проекция состояния на новую систему координат, повернутую на угол φ вокруг оси z, причем для определения направления поворота всегда применяется правило правой руки; R y (θ) означает, что оси координат повернуты на угол θ вокруг оси у . Зная эти два поворота, вы запросто сможете рассчитать любой поворот. Как обычно, матричный элемент пишется так, что состояние слева — это базисное состояние новой (повернутой) системы, а состояние справа — это базисное состояние старой (неповернутой) системы. Клетки таблицы можно истолковывать по-разному. К примеру, клетка e i φ/2в табл. 15.1 означает, что матричный элемент < — | R | —>=е -iφ/2. Но это означает также, что ^ R | —>=е -iφ/2|—> или что <���—| ^ R =<���—|e -iφ. Это все одно и то же.