Ричард Фейнман - Том 3. Квантовая механика

Вы помните также, что q вдвое больше заряда электрона, так что

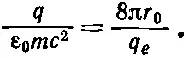
Записав ρ в виде q e N , где N — число электронов в кубическом сантиметре, мы получим

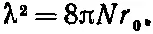(19.25)

У такого металла, как свинец, на каждый кубический сантиметр приходится 3·10 22атомов, и если каждый атом снабдит нас одним электроном проводимости, то 1/λ будет порядка 2·10 -5 см . Это дает вам порядок величины эффекта.

Уравнение Лондонов (19.21) было предложено, чтобы объяснить наблюдавшиеся при сверхпроводимости явления, включая эффект Мейсснера. Однако в последнее время прозвучали и более поразительные предсказания. Одно из предсказаний Лондонов было таким своеобразным, что никто даже не обратил на него особого внимания. Об этом я и расскажу. На сей раз возьмем сверхпроводящее кольцо, толщина которого по сравнению с 1/λ велика, и посмотрим, что случится, если мы сперва наложим на кольцо магнитное поле, затем охладим кольцо до сверхпроводящего состояния, а потом уберем первоначальный источник поля В. Последовательность этих событий изображена на фиг. 19.4.

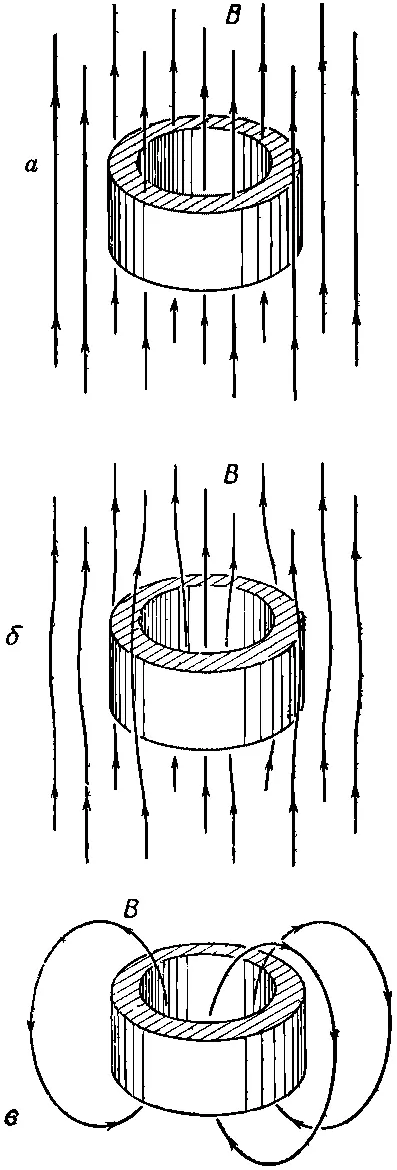
Фиг. 19,4. Кольцо в магнитном поле. а — в нормальном, состоянии; б — в сверхпроводящем состоянии; в — после того, как внешнее поле убрали.

В нормальном состоянии (фиг. 19.4, а ) в теле кольца имеется магнитное поле. Когда кольцо становится сверхпроводящим, поле (как мы уже знаем) выталкивается из вещества кольца. Но тогда, как показано на фиг. 19.4, б , останется некоторый поток поля сквозь отверстие кольца. Если теперь убрать внешнее поле, то те линии поля, которые шли через отверстие, будут «заморожены» (фиг. 19.4, в ). Поток Ф через центр сойти на нет не может, потому что ∂ Ф /∂ t должно быть все время равно контурному интегралу от Евдоль кольца, а Евнутри сверхпроводника равно нулю. И вот, когда мы убираем внешнее поле, то по кольцу начинает течь сверхпроводящий ток, цель которого — сохранить поток через кольцо неизменным. (Это старая идея о вихревых токах, только с нулевым сопротивлением.) Но все эти токи будут течь только у самой поверхности (на глубине не более 1/λ), что следует из такого же анализа, как и проделанный для сплошного куска. Эти токи в состоянии сделать так, чтобы магнитное поле не попадало внутрь кольца, но зато все время держалось вокруг него.

Но здесь имеется существенное различие, и наши уравнения предсказывают поразительный эффект. Рассуждение о том, что фаза θ в сплошном куске должна быть постоянной, к кольцу неприменимо ; в этом вам помогут убедиться следующие рассуждения.

Далеко в глубине тела кольца плотность тока Jравна нулю; значит, (19.18) означает, что

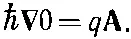(19.26)

Теперь посмотрим, что получится, если мы возьмем контурный интеграл от Апо кривой Г, которая проходит по самому центру поперечного сечения кольца, нигде не подходя близко к поверхности (фиг. 19.5).

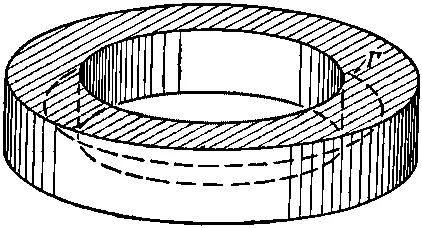
Фиг. 19.5. Кривая Г внутри сверхпроводникового кольца.

Из (19.26)

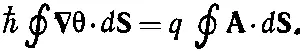(19.27)

Вы знаете, что контурный интеграл от Апо любой петле равен потоку Вчерез петлю

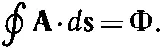
Стало быть, уравнение (19.27) превращается в

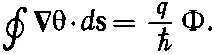(19.28)

Криволинейный интеграл от одной точки до другой (скажем, от точки 1 до точки 2) от градиента равен разности значений функции в этих двух точках:

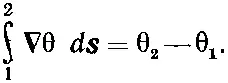
Если начать сближать точки 1 и 2, чтобы петля стала замкнутой, то на первый взгляд могло бы показаться, что θ 1станет равно θ 2, так что интеграл в (19.28) обратится в нуль. Так оно и было бы для замкнутых петель в односвязном куске сверхпроводника, но для кольцеобразного куска это не обязательно. Единственное физическое требование, которое мы вправе предъявить, это чтобы в каждой точке волновая функция могла принимать только одно значение . Что бы ни делала фаза θ, когда вы движетесь по кольцу, но когда вы возвращаетесь к начальной точке, фаза θ обязана обеспечить вам прежнее значение волновой функции ψ=√(ρe iθ). Так будет, если θ меняется на 2π n , где n — любое целое число. Итак, если мы делаем один полный оборот вокруг кольца, то левая часть (19.27) должна быть равна ℏ ·2π n . Подставляя сюда (19.28), получаем

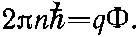(19.29)

Захваченный поток всегда обязан быть кратным числу 2πℏ/ q ! Если бы кольцо было классическим объектом с идеальной (т. е. бесконечной) проводимостью, то можно было бы подумать, что в кольце обязан остаться весь проходивший через него поток, какой бы величины он ни был, т. е. можно заморозить любое количество потока. Но квантовомеханическая теория сверхпроводимости утверждает, что поток может быть либо нулем, либо 2πℏ/ q , либо 4πℏ/ q , либо 6πℏ/ q и т. д., но только не промежуточным числом! Он обязан быть кратным фундаментальной квантовомеханической константе.

Лондон [96] F. London, Superfluids, Vol. 1, New York, 1950, p. 152. предсказывал, что поток, захватываемый сверхпроводящим кольцом, окажется квантованным и допустимая величина потока будет дана уравнением (19.29), где q = q e — заряду электрона. Согласно Лондону, фундаментальная единица потока должна быть равна 2πℏ/ q е, т. е. около 4·10 -7 гс · см 2. Чтобы представить себе эту величину, вообразите тонкий цилиндрик толщиной в одну десятую долю миллиметра; магнитное поле внутри него, если он содержит такую величину потока, составит около одного процента магнитного поля Земли. С помощью чувствительных магнитных измерений такой поток можно зарегистрировать.

В 1961 г. Дивер и Фейрбэнк [97] B. S. Deaver, Jr., W. M. Fairbank, Phys. Rev. Letters, 7, 43 (1961). из Станфордского университета предприняли поиски такого квантованного потока и нашли его; примерно в то же время это проделали Долл и Набауэр [98] R. Doll, M. Nabauer, Phys. Rev. Letters, 7, 51 (1961), в Германии.