Ричард Фейнман - Том 3. Квантовая механика

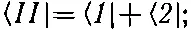
это означает то же самое, что и

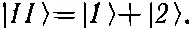(7.5)

Амплитуда того, что состояние |II> окажется в состоянии |1>, равна

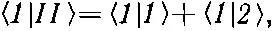
а это, конечно, равняется просто единице, поскольку и |1>, и |2> суть базисные состояния. И амплитуда обнаружения состояния |II> в состоянии |2> тоже равна единице, так что у состояния |II> одинаковы амплитуды оказаться в каждом из базисных состояний |1> и |2>.

Но тут всплывает новая трудность. У состояния | II > полная вероятность оказаться то ли в одном базисном состоянии, то ли в другом получается больше единицы. Но это всего лишь означает, что вектор состояния неудачно «отнормирован». Чтобы исправить дело, надо вспомнить, что всегда для любого состояния обязано быть < II | II >=1. Использовав общее соотношение

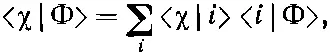
полагая, что и Ф, и χ суть состояние II, и суммируя по базисным состояниям |1> и |2>, получаем

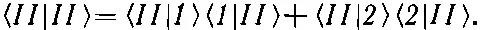
Это даст, как положено, единицу, если мы изменим наше определение С II [см. уравнение (7.4)] и примем

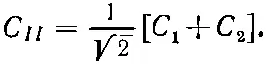
Таким же путем можно построить и амплитуду

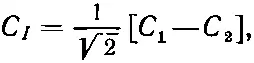
или

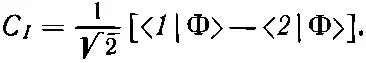(7.6)

Эта амплитуда есть проекция состояния |Ф> на новое состояние | I >, обладающее амплитудами противоположного знака, для пребывания в состояниях |1> и |2>. А именно (7.6) означает то же самое, что и

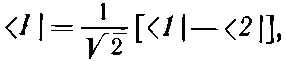
или

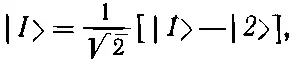(7.7)

откуда следует

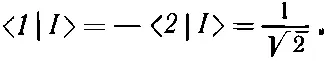
Зачем все это нужно? С какой целью все это делается? Дело в том, что состояния |I> и |II> могут быть приняты за новую совокупность базисных состояний , особенно подходящую для описания стационарных состояний молекулы аммиака. Вы помните, что требования к совокупности базисных состояний были таковы:

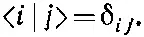
Мы уже сами сделали так, чтобы было

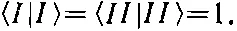
Из (7.5) и (7.7) легко вывести, что и

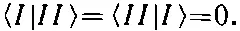
Амплитуды С I =< I |Ф> и С II =< II |Ф> того, что любое состояние |Ф> окажется в одном из наших новых базисных состояний | I > и | II >, обязаны также удовлетворять гамильтонову уравнению вида (6.39). И действительно, если мы просто вычтем друг из друга два уравнения (7.2) и (7.3) и продифференцируем по t , то убедимся, что

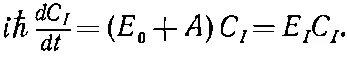(7.8)

А взяв сумму (7.2) и (7.3), увидим

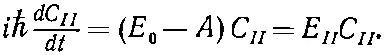(7.9)

Если за базисные состояния взять | I > и | II >, то гамильтонова матрица очень проста:

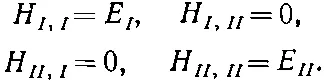
Заметьте, что каждое из уравнений (7.8) и (7.9) выглядит очень похоже на то, что получалось в гл. 6, § 6, для уравнения системы с одним состоянием. Они дают простую экспоненциальную зависимость от времени, отвечающую определенной энергии. С ростом времени амплитуды пребывания в каждом из состояний ведут себя независимо.

Найденные нами раньше стационарные состояния |ψ I> и |ψ II> тоже являются, конечно, решениями уравнений (7.8) и (7.9). У состояния |ψ I> (для которого С 1=- С 2)

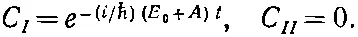(7.10)

А у состояния |ψ II> (для которого С 1= С 2)

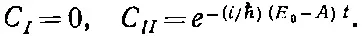(7.11)

Пусть мы теперь умножили (7.10) на вектор состояния | I >; тогда получится

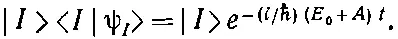
Вспомним, однако, что |I>

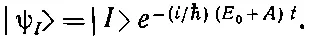
Иначе говоря, вектор состояния стационарного состояния |ψ I> не отличается от вектора состояния базисного состояния | I > ничем, кроме экспоненциального множителя, связанного с энергией состояния. И действительно, при t=0

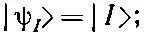
физическая конфигурация у состояния | I > та же самая, что и у стационарного состояния с энергией Е 0+ А . Точно так же для второго стационарного состояния получается

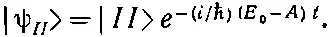
Состояние | II >— это просто стационарное состояние с энергией Е 0- А при t =0. Стало быть, оба наших новых базисных состояния | I > и | II > физически имеют вид состояний с определенной энергией, но с изъятым экспоненциальным временным множителем, так что они могут быть приняты за базисные состояния, не зависящие от времени. (В дальнейшем нам будет удобно не отличать стационарные состояния |ψ I> и |ψ II> от их базисных состояний | I > и | II >, ведь различаются они только очевидными временными множителями.)

Подведем итог. Векторы состояний | I > и | II > — это пара базисных векторов, приспособленных для описания состояний молекулы аммиака с определенной энергией. Они связаны с нашими исходными базисными векторами формулами