Ричард Фейнман - Том 3. Квантовая механика

Как же разделить два молекулярных состояния? Один способ такой. Аммиачный газ выпускается тонкой струйкой и проходит через пару щелей, создающих узкий пучок (фиг. 7.3).

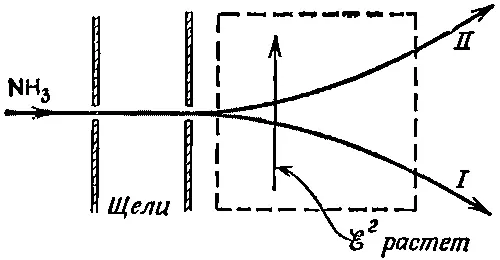
Фиг. 7.3. Пучок молекул аммиака может быть разделен электрическим полем, в котором ℰ 2 обладает градиентом, перпендикулярным пучку.

Затем пучок пропускается через область, в которой имеется сильное поперечное электрическое поле. Создающие поле электроды изогнуты так, чтобы электрическое поле поперек пучка резко менялось. Тогда квадрат ℰ·ℰ электрического поля будет иметь большой градиент, перпендикулярный пучку. А у молекулы в состоянии | I > энергия с ℰ 2растет, значит, эта часть пучка отклонится в область меньших ℰ 2. Молекула же в состоянии | II >, наоборот, отклонится к области, где ℰ 2побольше, потому что ее энергия падает, когда ℰ 2растет.

Кстати, при тех электрических полях, которые удается генерировать в лаборатории, энергия μℰ всегда много меньше А . В этом случае корень в уравнении (7.30) приближенно равен

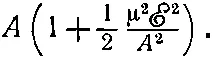(7.32)

Во всех практических случаях энергетические уровни, стало быть, равны

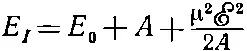(7.33)

и

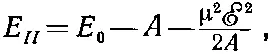(7.34)

и энергии с ℰ 2меняются линейно. Действующая на молекулы сила тогда равна

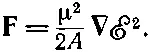(7.35)

Энергия в электрическом поле у многих молекул пропорциональна ℰ 2. Коэффициент — это поляризуемость молекулы. Поляризуемость аммиака необычно высока: у него А в знаменателе очень мало. Стало быть, молекулы аммиака очень чувствительны к электрическому полю.

В аммиачном мазере пучок молекул в состоянии | I > и с энергией Е I пропускается через резонансную полость, как показано на фиг. 7.4.

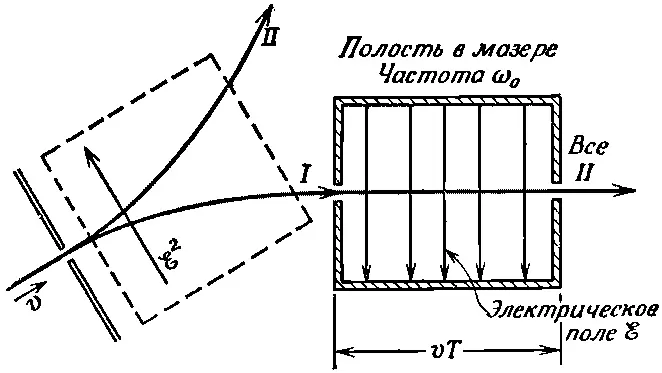
Фиг. 7.4. Схематическое изображение аммиачного мазера.

Другой пучок отводится прочь. Внутри полости существует меняющееся во времени электрическое поле, так что нашей очередной задачей явится изучение поведения молекулы в электрическом поле, которое меняется во времени. Это совершенно новый род задач — задача с гамильтонианом, меняющимся во времени. Раз H ij зависит от ℰ, то и H ij меняется во времени, и нам надлежит определить поведение системы в этих обстоятельствах.

Для начала выпишем уравнения, которые нужно решить:

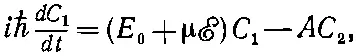(7.36)

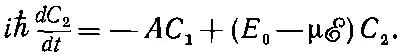
Для определенности положим, что электрическое поле меняется синусоидально; тогда можно написать

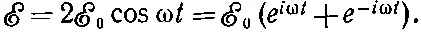(7.37)

На самом деле частота ω берется всегда очень близкой к резонансной частоте молекулярного перехода ω 0=2 A / ℏ , но пока мы для общности будем считать ω произвольной. Лучший способ решить наши уравнения — это, как и прежде, составить из C 1и С 2линейные комбинации. Сложим поэтому оба уравнения, разделим на √2 и вспомним определения С I и С II из (7.13). Получим

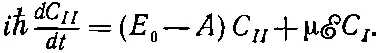(7.38)

Вы видите, что это похоже на (7.9), но появился добавочный член от электрического поля. Равным образом, вычитая уравнения (7.36), получаем

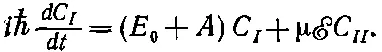(7.39)

Вопрос теперь в том, как решить эти уравнения. Это труднее, чем прежде, потому что ℰ зависит от t ; и действительно, при общем ℰ( t ) решение не представимо в элементарных функциях. Однако, пока электрическое поле мало, можно добиться хорошего приближения. Сперва напишем

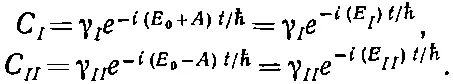(7.40)

Если бы электрического поля не было, то, беря в качестве γ I и γ II две комплексные постоянные, мы бы получили правильное решение. Ведь поскольку вероятность быть в состоянии | I > есть квадрат модуля C I , а вероятность быть в состоянии | II > есть квадрат модуля С II , то вероятность быть в состоянии | I > или в состоянии | II > равна просто |γ I | 2или |γ II | 2. Например, если бы система начинала развиваться из состояния | II > так, что γ I было бы нулем, а |γ II | 2— единицей, то эти условия сохранились бы навсегда. Молекула из состояния | II > никогда бы не перешла в состояние | I >.

Польза записи решений в форме (7.40) состоит в том, что оно сохраняет свой вид и тогда, когда есть электрическое поле, если только μℰ меньше А , только γ I и γ II при этом станут медленно меняющимися функциями времени. «Медленно меняющиеся» означает медленно в сравнении с экспоненциальными функциями. В этом весь фокус. Для получения приближенного решения используется тот факт, что γ I и γ II меняются медленно.

Подставим теперь С I из (7.40) в дифференциальное уравнение (7.39), но вспомним, что γ I тоже зависит от t . Имеем

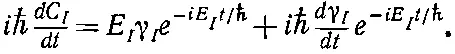
Дифференциальное уравнение обращается в

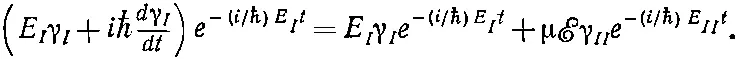(7.41)

Равным образом уравнение для dC II / dt обращается в

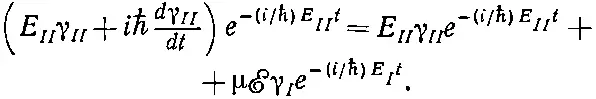(7.42)

Обратите теперь внимание, что в обеих частях каждого уравнения имеются одинаковые члены. Сократим их и умножим первое уравнение на exp (+ E I t / ℏ ), а второе на exp (+ E II t / ℏ ). Вспоминая, что ( E I - E ii )=2 А = ℏ ω 0, мы в конце концов получаем