Ричард Фейнман - Том 3. Квантовая механика

Поскольку это решение отвечает состоянию с энергией E = ℏ ω, то можно прямо написать

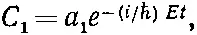(7.18)

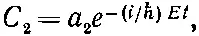(7.19)

где Е пока неизвестна и должна быть определена так, чтобы дифференциальные уравнения (7.16) и (7.17) выполнялись. При подстановке С 1и С 2из (7.18) и (7.19) в дифференциальные уравнения (7.16) и (7.17) производные дают просто - iE / ℏ , умноженное на С 1или C 2, так что слева остается попросту ЕС 1или ЕС 2. Сокращая общие экспоненциальные множители, получаем

или после перестановки членов

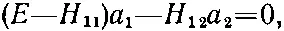(7.20)

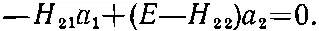(7.21)

У такой системы однородных алгебраических уравнений ненулевые решения для а 1и а 2будут лишь тогда, когда определитель, составленный из коэффициентов при а 1и а 2, равен нулю, т. е. если

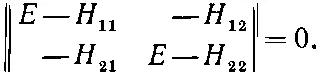(7.22)

Но когда уравнений два и неизвестных тоже два, то можно обойтись и без столь возвышенных представлений. Каждое из уравнений (7.20) и (7.21) дает отношение двух коэффициентов a 1и а 2, и эти два отношения должны быть равны. Из (7.20) мы имеем

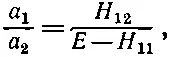(7.23)

а из (7.21)

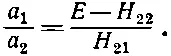(7.24)

Приравнивая эти отношения, получаем, что Е должно удовлетворять равенству

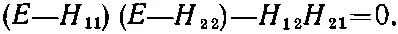
То же получилось бы и из (7.22). В любом случае для Е получается квадратное уравнение с двумя решениями:

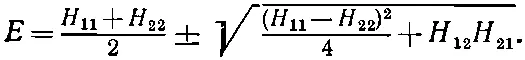(7.25)

Энергия E может иметь два значения. Заметьте, что оба они вещественны , потому что Н 11и H 22вещественны, а Н 12 Н 21, равное Н 12 H 12=| H 12| 2, тоже вещественно, да к тому же положительно.

Пользуясь тем же соглашением, что и раньше, обозначим большую энергию E I , а меньшую Е II . Имеем

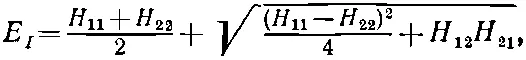(7.26)

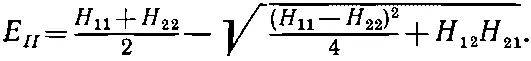(7.27)

Подставив каждую из этих энергий по отдельности в (7.18) и (7.19), получим амплитуды для двух стационарных состояний (состояний определенной энергии). Если нет каких-либо внешних возмущений, то система, первоначально бывшая в одном из этих состояний, останется в нем навсегда, у нее только фаза будет меняться.

Наши результаты можно проверить на двух частных случаях. Если H 12= H 21=0, то получается E I = H 11и E II = H 22. А это бесспорно правильно, потому что тогда уравнения (7.16) и (7.17) не связаны и каждое представляет состояние с энергией H 11и H 22. Далее, положив H 11= H 22= E 0и H 21= H 12=- А , придем к найденному выше решению:

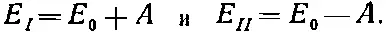
В общем случае два решения Е I и Е II относятся к двум состояниям; мы их опять можем назвать состояниями

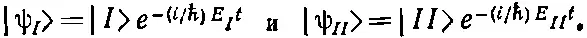
У этих состояний С 1и С 2будут даваться уравнениями (7.18) и (7.19), где а 1и а 2еще подлежат определению. Их отношение дается либо формулой (7.23), либо (7.24). Они должны также удовлетворять еще одному условию. Если известно, что система находится в одном из стационарных состояний, то сумма вероятностей того, что она окажется в |1> или |2>, должна равняться единице. Следовательно,

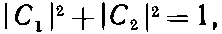(7.28)

или, что то же самое,

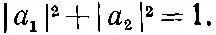(7.29)

Эти условия не определяют а 1и а 2однозначно: остается еще произвол в фазе, т. е. в множителе типа е i δ. Хотя для а можно выписать общие решения [23] Например, как легко убедиться, одно из допустимых решений имеет вид , но обычно удобнее вычислять их в каждом отдельном случае.

Вернемся теперь к нашему частному примеру молекулы аммиака в электрическом поле. Пользуясь значениями Н 11, H 22и Н 12из (7.14) и (7.15), мы получим для энергий двух стационарных состояний выражения

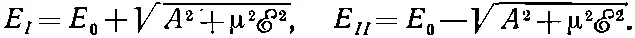(7.30)

Эти две энергии как функции напряженности ℰ электрического поля изображены на фиг. 7.2.

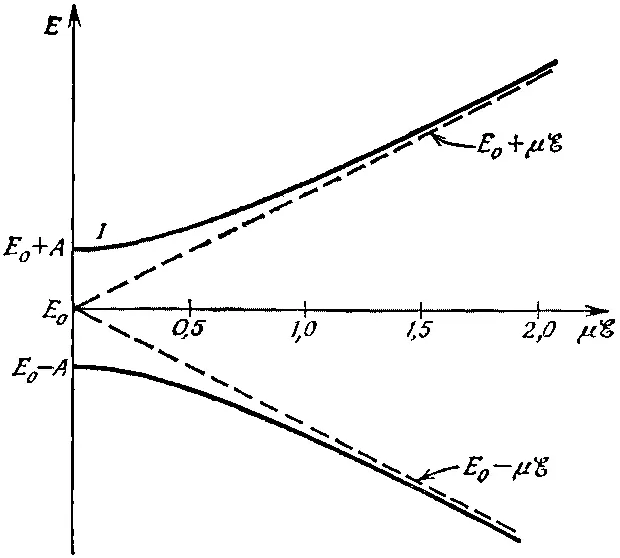
Фиг. 7.2. Уровни энергии молекулы аммиака в электрическом поле. Кривые построены по формулам (7.30): E=E0±√(A 2 +μ 2 ℰ 2 ).

Когда электрическое поле нуль, то энергии, естественно, обращаются в Е 0± А . При наложении электрического поля расщепление уровней растет. Сперва при малых ℰ оно растет медленно, но затем может стать пропорциональным ℰ. (Эта линия — гипербола.) В сверхсильных полях энергии попросту равны

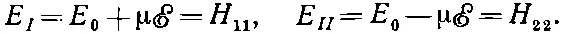(7.31)

Тот факт, что у азота существует амплитуда переброса вверх — вниз, малосуществен, когда энергии в этих двух положениях сильно отличаются . Это интересный момент, к которому мы позже еще вернемся.

Теперь мы наконец готовы понять действие аммиачного мазера. Идея в следующем. Во-первых, мы находим способ отделения молекул в состоянии | I > от молекул в состоянии | II > [24] Теперь мы опять будем писать | I > и | II > вместо |ψ I > и |ψ II >. Вы должны вспомнить, что настоящие состояния |ψ I > и |ψ II > суть энергетические базисные состояния, умноженные на соответствующий экспоненциальный множитель. . Затем молекулы в высшем энергетическом состоянии | I > пропускаются через полость, у которой резонансная частота равна 24000 Мгц . Молекулы могут оставить свою энергию полости (способ будет изложен позже) и покинуть полость в состоянии | II >. Каждая молекула, совершившая такой переход, передаст полости энергию E = E I - Е II . Энергия, отобранная у молекул, проявится в виде электрической энергии полости.