Ричард Фейнман - Том 3. Квантовая механика

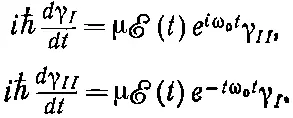(7.43)

Получилась довольно простая пара уравнений — и пока еще точная. Производная от одной переменной есть функция от времени μ ℰ ( t ) exp ( i ω 0 t ), умноженная на вторую переменную; производная от второй — такая же функция от времени, умноженная на первую. Хотя эти простые уравнения в общем не решаются, но в некоторых частных случаях мы решим их.

Нас, по крайней мере сейчас, интересует только случай колеблющегося электрического поля. Взяв ℰ( t ) в форме (7.37), мы увидим, что уравнения для γ I и γ II обратятся в

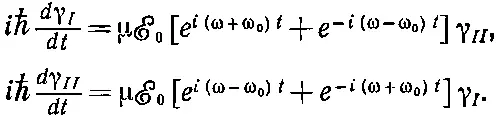(7.44)

И вот если ℰ 0достаточно мало, то скорости изменения γ I и γ II тоже будут малы. Обе γ не будут сильно меняться с t , особенно в сравнении с быстрыми вариациями, вызываемыми экспоненциальными членами. У этих экспоненциальных членов есть вещественные и мнимые части, которые колеблются с частотой ω+ω 0или ω-ω 0. Члены с частотой ω+ω 0колеблются вокруг среднего значения (нуля) очень быстро и поэтому не дадут сильного вклада в скорость изменения γ. Значит, можно сделать весьма разумное приближение, заменив эти члены их средним значением, т. е. нулем. Их просто убирают и в качестве приближения берут

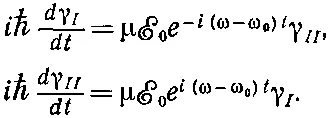(7.45)

Но даже и оставшиеся члены с показателями, пропорциональными (ω-ω 0), меняются быстро, если только ω не близко к ω 0. Только тогда правая сторона будет меняться достаточно медленно для того, чтобы набежало большое число, пока интегрируешь эти уравнения по t . Иными словами, при слабом электрическом поле изо всех частот представляют важность лишь те, которые близки к ω 0.

При тех приближениях, которые были сделаны для того, чтобы получить (7.45), эти уравнения можно решить и точно; но работа эта все же трудоемкая, и мы отложим ее на другое время, когда обратимся к другой задаче того же типа. Пока же мы их просто решим приближенно, или, лучше сказать, найдем точное решение для случая идеального резонанса ω=ω 0и приближенное — для частот близ резонанса.

Первым рассмотрим случай идеального резонанса. Если положить ω=ω 0, то экспоненты в обоих уравнениях (7.45) станут равными единице, и мы просто получим

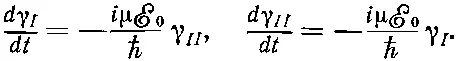(7.46)

Если из этих уравнений исключить сперва γ I , а потом γ II , то мы увидим, что каждое из них удовлетворяет дифференциальному уравнению простого гармонического движения

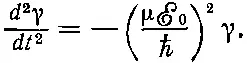(7.47)

Общее решение этих уравнений может быть составлено из синусов и косинусов. Легко проверить, что решениями являются следующие выражения:

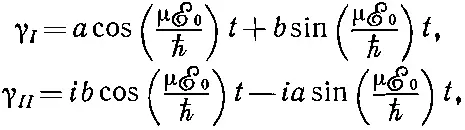(7.48)

где а и b — константы, которые надо еще определить так, чтобы они укладывались в ту или иную физическую ситуацию.

К примеру, предположим, что при t =0 наша молекулярная система была в верхнем энергетическом состоянии | I >, а это требует [из уравнения (7.40)], чтобы γ I =1 и γ II =0 при t =0. Для такого случая должно быть а =1 и b =0. Вероятность того, что молекула окажется в том же состоянии | I > в какой-то позднейший момент t , равна квадрату модуля γ I , или

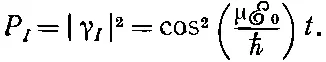(7.49)

Точно так же и вероятность того, что молекула окажется в состоянии | II >, дается квадратом модуля γ II :

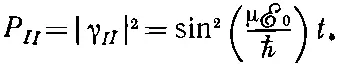(7.50)

Пока ℰ мало и пока мы находимся в резонансе, вероятности даются простыми колебательными функциями. Вероятность быть в состоянии | I > падает от единицы до нуля и возрастает опять, а вероятность быть в состоянии | II > растет от нуля до единицы и наоборот. Изменение обеих вероятностей во времени показано на фиг. 7.5.

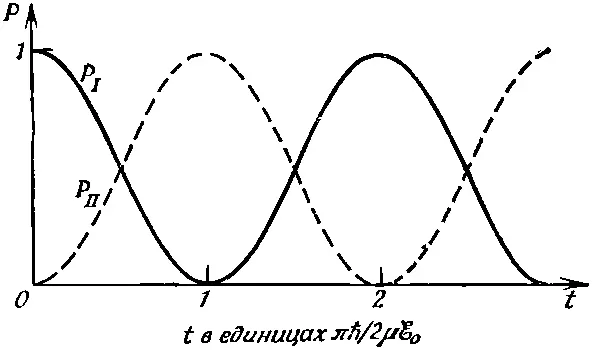
Фиг. 7.5. Вероятности обоих состояний молекулы аммиака в синусоидальном электрическом поле.

Нечего и говорить, что сумма обеих вероятностей всегда равна единице; ведь молекула всегда находится в каком - то состоянии.

Положим, что прохождение через полость занимает у молекулы время Т . Если сделать полость как раз такой длины, чтобы было μℰ 0 Т / ℏ =π/2, то молекула, ныряющая в нее в состоянии | I >, наверняка вынырнет из нее в состоянии | II >. Если она вошла в полость в верхнем состоянии, то выйдет из полости в нижнем. Иными словами, ее энергия упадет, и эта потеря энергии не сможет перейти ни во что другое, а только в механизм, который генерирует поле. Детали, которые помогли бы вам разглядеть, как именно энергией молекулы питаются колебания полости, не так уж просты; однако нам и не нужно все эти детали изучать, потому что имеется принцип сохранения энергии. (Мы могли бы, если бы это было нужно, изучить их, но тогда нам пришлось бы иметь дело с квантовой механикой поля в полости наряду с квантовой механикой атома.)

Подытожим. Молекула входит в полость, поле полости, колеблющееся с как раз нужной частотой, индуцирует переходы с верхнего состояния на нижнее, и высвобождаемой энергией питается осциллирующее поле. В работающий мазер молекулы доставляют достаточно энергии для того, чтобы поддерживались колебания полости, ее хватает не только на то, чтобы возместить потери в полости, но и на то, чтобы небольшие избытки энергии извлекались из полости. Итак, молекулярная энергия превращается в энергию внешнего электромагнитного поля.

Вспомним, что перед входом в полость нам приходилось пользоваться фильтром, который разделял пучок так, что в полость входило только верхнее состояние. Легко показать, что, если бы мы начали с молекул в нижнем состоянии, процесс пошел бы в другую сторону и энергия от полости отбиралась бы. Если пустить в полость нефильтрованный пучок, то сколько молекул будет отбирать энергию от полости, столько же из них будет отдавать ей свою энергию, и в итоге ничего не случится. В настоящем мазере, конечно, не обязательно делать (μℰ 0T/ ℏ ) точно равным π/2. И при других значениях (кроме точных кратных π) существует какая-то вероятность переходов из состояния | I > в состояние | II >. Но при этих других значениях прибор уже не имеет к. п. д., равного 100%; многие из молекул, покидающие полость, могли бы снабдить ее энергией, но не сделали этого.