Ричард Фейнман - Том 3. Квантовая механика

Еще немного о том, как можно применить те же идеи, чтобы понять, что происходит с электроном в трех измерениях. Результаты оказываются очень похожими. Пусть имеется прямоугольная решетка атомов с расстояниями а, b, с в трех направлениях. (Если вам больше по душе кубическая решетка, примите все расстояния равными друг другу.) Предположим также, что амплитуда прыжка к соседу в направлении х есть iA x / ℏ ; амплитуда прыжка в направлении у есть iA y / ℏ , а амплитуда прыжка в направлении z есть iA z / ℏ . Как же описать базисные состояния? Как и в одномерном случае, одно базисное состояние — это когда электрон находится близ атома с координатами х, у, z , где ( х, у, z ) — одна из точек решетки. Если выбрать начало координат в одном из атомов, то все эти точки придутся на

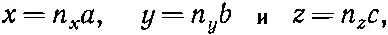
где n х , n y , n z — три целых числа. Вместо того чтобы ставить при х, у и z их номера, будем просто писать х, у , z, имея в виду, что они принимают лишь такие значения, которые бывают у точек решетки. Итак, базисное состояние изображается символом |электрон в х, у , z>, а амплитуда того, что электрон в некотором состоянии |ψ> окажется в этом базисном состоянии, есть

С ( х, у , z)=<���электрон в х, у, z |ψ>.

Как и прежде, амплитуды С ( х, у , z) могут меняться во времени. При наших предположениях гамильтоновы уравнения обязаны выглядеть следующим образом:

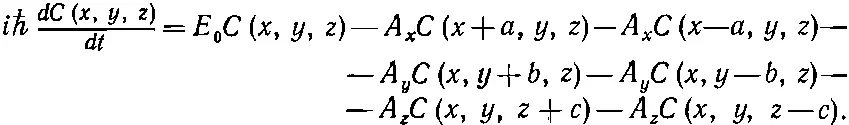(11.22)

Хоть это и выглядит громоздко, но вы сразу, конечно, поймете, откуда взялось каждое слагаемое.

Опять попробуем найти стационарное состояние, в котором все С меняются со временем одинаково. И снова решение есть экспонента

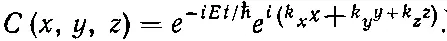(11.23)

Если вы подставите это в (11.22), то увидите, что оно вполне подойдет, если только энергия Е будет связана с k x , k y и k z следующим образом:

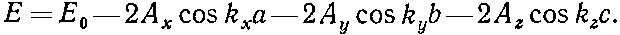(11.24)

Теперь энергия зависит от трех волновых чисел k x , k y , k z , которые, кстати, есть компоненты трехмерного вектора k. И действительно, (11.23) можно переписать в векторных обозначениях:

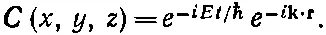(11.25)

Амплитуда меняется как комплексная плоская волна , которая движется в трехмерном пространстве в направлении kс волновым числом k =( k x 2+ k y 2+ k z 2) 1/2.

Энергия, связываемая с этими стационарными состояниями, зависит от трех компонент kсложным образом, подчиняясь уравнению (11.24). Характер изменения Е зависит от относительных знаков и величин А х , А у и А z . Если вся эта тройка положительна и если нас интересуют лишь маленькие k, то зависимость оказывается сравнительно простой.

Разлагая косинус, как и раньше [см. (11.16)], мы теперь придем к

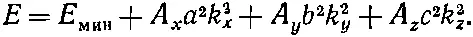(11.26)

В простой кубической решетке с расстоянием а между узлами следует ожидать, что и А х , и А y , и А г будут все равны друг другу (скажем, равны А ), так что получилось бы

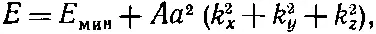(11.27)

или

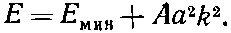
А это как раз совпадает с (11.16). Повторяя те же рассуждения, что и тогда, мы пришли бы к заключению, что электронный пакет в трех измерениях (составленный путем суперпозиции множества состояний с почти одинаковыми энергиями) также движется на манер классической частицы, обладающей некоторой эффективной массой.

В кристалле не с кубической, а с более низкой симметрией (или даже в кубическом кристалле, но таком, в котором состояние электрона около атома несимметрично) три коэффициента А х , А y и A z различны. Тогда «эффективная масса» электрона, сосредоточенного в узкой области, зависит от направления его движения . Может, например, оказаться, что у него разная инерция при движении в направлении х и при движении в направлении у . (Детали такого положения вещей иногда описываются с помощью «тензора эффективной массы».)

Согласно (11.24), состояния электрона, о которых мы говорили, могут обладать энергиями только в некоторой энергетической «полосе», простирающейся от наименьшей энергии

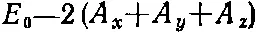
до наибольшей

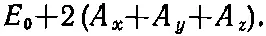
Другие энергии тоже возможны, но они принадлежат к другому классу состояний электрона. Для тех состояний, о которых говорилось раньше, мы выбирали такие базисные состояния, когда электрон в атоме кристалла находился в некотором определенном состоянии, скажем в состоянии наинизшей энергии.

Если у вас есть атом в пустом пространстве и вы добавляете к нему электрон, чтобы получился ион, то этот ион можно образовать многими способами. Электрон может расположиться так, чтобы образовать состояние наинизшей энергии, или так, чтобы образовать то или иное из многих возможных «возбужденных состояний» иона, каждое с определенной энергией, которая превосходит наинизшее значение. То же может случиться и в кристалле. Допустим, что энергия Е 0, которой мы пользовались выше, соответствует базисным состояниям, представляющим собой ионы с наинизшей возможной энергией. Но можно также вообразить новую совокупность базисных состояний, в которых электрон по-иному располагается возле n -го атома: он образует одно из возбужденных состояний иона, так что энергия Е 0теперь уже становится чуть повыше. Как и раньше, имеется некоторая амплитуда А (отличная от прежней) того, что электрон перепрыгнет из своего возбужденного состояния близ одного атома в такое же возбужденное состояние подле соседнего атома. И весь анализ проходит, как раньше; мы обнаружим полосу возможных энергий, сосредоточенных вокруг некоторой высшей энергии. Вообще говоря, таких полос может быть много и каждая будет отвечать своему уровню возбуждения.