Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]

Мелкие тела имеются и в других местах Солнечной системы, но первые несколько открытий добавили весомости мнению Боде о том, что планеты распределены в ней регулярно. Последовавшее открытие Нептуна было мотивировано возмущениями в орбите Урана, а не законом Тициуса — Боде. Но закон предсказывал расстояние 38,8 а.е., что более или менее соответствует реальному расстоянию — где-то между 29,8 и 30,3. Попадание, конечно, не слишком точное, но приемлемое. Затем настала очередь Плутона: теоретическое расстояние 77,2; реальное — от 29,7 до 48,9. Вот и все, закон Тициуса — Боде перестал действовать.

Другие типичные черты планетарных орбит тоже оказались неуниверсальными. Плутон, скажем, очень странная планета. Его орбита обладает высоким эксцентриситетом и наклонена на чудовищные 17° к эклиптике. Иногда Плутон даже заходит внутрь орбиты Нептуна. Все эти нестандартные черты недавно привели к тому, что Плутон был разжалован из настоящих планет в карликовые. В качестве частичной компенсации Церера тоже стала карликовой планетой, а не просто астероидом (или малой планетой) [25] При этом никто не обратил внимания на чисто языковую нестыковку: что в английском, что в русском языке карликовая планета (dwarf planet) интуитивно воспринимается как менее значимый объект, нежели малая планета (minor planet). — Прим. ред. .

Несмотря на все успехи и неудачи, закон Тициуса — Боде ставит перед нами важные вопросы: имеет ли распределение планет какое-то математическое обоснование? Или они могли в принципе расположиться вокруг Солнца любым желаемым образом, на любых расстояниях? Что представляет собой этот закон — совпадение, проявление какой-то неизвестной закономерности или то и другое одновременно?

В качестве первого шага переформулируем закон Тициуса — Боде в более общий и слегка модифицированный вид. В оригинальной форме этот закон имеет аномалию: в качестве первого члена последовательности в нем используется 0. В полноценной геометрической прогрессии на этом месте должно было бы стоять 1,5. Хотя при таком выборе расстояние до Меркурия становится 0,55 (что менее точно), вся наша игра с расстояниями имеет чисто эмпирический и приближенный характер, так что, пожалуй, разумнее будет сохранить математическую аккуратность и использовать 1,5. Теперь закон можно выразить простой формулой: расстояние от Солнца до n -й планеты в астрономических единицах равно

d = 0,075 × 2 n+ 0,4.

Теперь следует провести несколько вычислений. По большому счету 0,4 а.е. для отдаленных планет не играет особой роли, поэтому отбросим этот член и получим d = 0,075 × 2 n. Это уже center степенного закона, который в общем виде записывается как d = ab n, где a и b — константы.

Прологарифмируем уравнение:

log d = log a + n log b.

Если интерпретировать n и log d как координаты, получим уравнение прямой с наклоном log b , пересекающей вертикальную ось в точке log a . Таким образом, чтобы распознать степенную зависимость, нужно построить график зависимости log d от n в логарифмическом масштабе по обеим осям. Если результат окажется близок к прямой, все в порядке. Мало того, мы можем проделать то же самое не только для расстояния d , но и для других величин, таких как период обращения вокруг звезды или масса.

Если попытаться проделать это для расстояний от Солнца до планет, включая Цереру и Плутон, то получится график на рисунке слева. Он близок к прямой, как и следовало бы ожидать по закону Тициуса — Боде. А как насчет их масс (смотрим на рисунок справа)? На этот раз полулогарифмический график выглядит совершенно иначе. Ничего похожего на прямую или какую бы то ни было другую четкую зависимость.

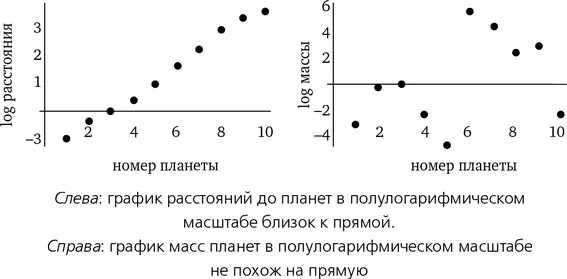
А орбитальный период? Вновь чистая прямая (смотри следующий график слева). Однако это неудивительно, поскольку третий закон Кеплера соотносит период с расстоянием таким образом, что степенная зависимость сохраняется. Попробуем расширить поле исследования и проверим пять основных лун Урана; получим график справа. Вновь степенная зависимость.

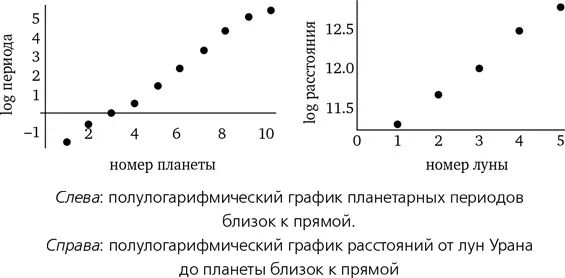
Совпадение или что-то более глубокое? Мнения астрономов разделились. В лучшем случае наблюдается тенденция к степенной зависимости в расстояниях. При этом зависимость не универсальна.

Здесь вполне возможно какое-то рациональное объяснение. Наиболее вероятное начинается с идеи о том, что в динамике случайной системы планет принципиально важную роль играют резонансы — случаи, когда орбитальные периоды двух планет дают в отношении простую дробь. К примеру, один из периодов может составлять 3/5 от другого, это резонанс 5:3 [26] Из примечания к главе 2 можно узнать, почему мы не называем такой резонанс 3:5. . Не обращая внимания на остальные тела, эти две планеты будут то и дело — через правильные интервалы — выстраиваться вдоль радиальной прямой, связывающей их со звездой, потому что пять оборотов одной планеты вокруг звезды в точности соответствуют трем оборотам другой планеты. За долгий период времени возникающие при этом небольшие возмущения орбит будут накапливаться, так что планеты будут склонны менять свои орбиты. В то же время для периодов, отношение которых не дает простой дроби, возмущения, как правило, компенсируются, поскольку в таких системах нет преимущественного направления, вдоль которого могла бы действовать связывающая две планеты сила тяготения.

И это не просто неопределенное предположение: оно подтверждается детальными расчетами и обширной математической теорией. В первом приближении орбита небесного тела представляет собой эллипс. На следующем уровне аппроксимации наблюдается прецессия эллипса: его большая ось медленно поворачивается в пространстве. Еще более точная аппроксимация показывает, что доминирующие члены в centerх движения небесных тел возникают от вековых (секулярных) резонансов — более общего типа резонансных отношений между периодами, с которыми прецессируют орбиты нескольких тел.

Как именно движутся тела, находящиеся в резонансе друг с другом, зависит от отношения периодов, а также от их координат и скоростей, но часто результатом бывает очищение подобных орбит. Компьютерное моделирование показывает, что случайным образом распределенные вокруг звезды планеты склонны занимать позиции, отношения между которыми примерно похожи на закон Тициуса — Боде, а промежуточные позиции вычищаются резонансами. Но все это достаточно неопределенно и расплывчато.