Айзек Азимов - Популярная физика. От архимедова рычага до квантовой механики

Крутящие моменты, используемые при применении рычага, часто образуются под действием грузов, опирающихся на концы балансировочного рычага; они также могут находиться на чашках, установленных на этих концах. Можно сказать, что два равных груза приведут рычаг в положение равновесия, если они помещены на противоположные стороны точки опоры и на равных расстояниях от нее.

Это фактически и является принципом «балансирных весов». Такие весы имеют две чашки равного веса, установленные на концах горизонтального прутка («коромысла», поэтому такие весы также называют «весами с коромыслом». — Пер.), который вращается относительно центральной точки опоры. Если мы поместим объект неизвестного веса в одну чашку, а в другую чашку — набор известных весов (тарированные гирьки) и приведем весы в положение равновесия, то неизвестный вес будет равен сумме известных весов в другой чашке. По этому же принципу мы измеряем массу, а не только вес.

Рычаг, подвергнутый воздействию равных и противоположных по знаку крутящих моментов, считается находящимся «в положении равновесия» («equilibrum» — от латинских слов, означающих «равные веса»). Это выражение применяют к любой системе, находящейся под воздействием сил, которые производят взаимоисключающие эффекты и оставляют общее состояние системы неизменным.

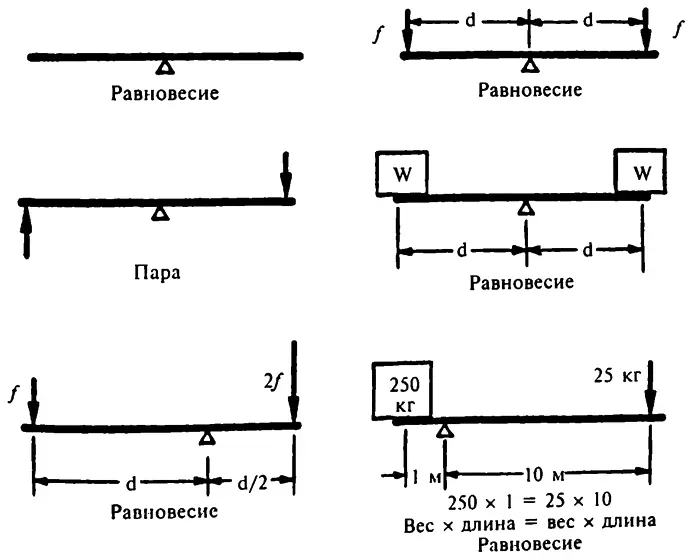
Для того чтобы рычаг находился в положении равновесия, он должен быть подвергнут воздействию равных и противоположных по знаку крутящих моментов, и это справедливо даже в том случае, если приложенные силы неравны. Рассмотрим направленную вниз силу f), приложенную к точке на одной стороне рычага на некотором расстоянии (к) от точки опоры. Крутящий момент, создаваемый этой силой, равен fr. Затем рассмотрим другую направленную вниз силу, величиной вдвое больше, чем первая (2f), приложенную к точке на другой стороне от точки опоры, но на расстоянии, равном только половине первого (–r/2). (Мы ставим отрицательный знак перед величиной расстояния потому, что это расстояние находится на противоположном от точки опоры направлении относительно первого.) Этот второй крутящий момент равен (2f)∙(–r/2) или (–fr). То есть мы имеем два крутящих момента, которые равны и противоположны, и рычаг остается в положении равновесия.

Легко видеть, что если силы произведены неравными весами, опирающимися на концы рычага, то центр тяжести системы должен сместиться к концу с большим весом. Чтобы поддерживать равновесие, точка опоры должна находиться непосредственно под новым положением центра тяжести. Как только это будет сделано, мы сразу сможем обнаружить, что его положение центра тяжести стало таким, что произведение одного веса на его расстояние от точки опоры стало равно произведению другого веса на его расстояние от точки опоры.

Таким образом, если два ребенка примерно равного веса находятся на качелях, правильным для них будет сесть на концы качелей. Если один ребенок заметно более тяжелый, чем другой, он должен сидеть ближе к точке опоры. Эти двое детей должны расположиться таким образом, чтобы их собственный центр тяжести плюс таковой качелей находился непосредственно над точкой опоры. (В устройстве некоторых качелей предусмотрена возможность перемещения, то есть имеется регулировка длины коромысла для «подстройки» его положения по отношению к точке опоры.)

Тот факт, что для равновесия системы требуется равенство крутящих моментов, а не сил, определил широкое использование рычага. Предположим, что мы поместили вес в 250 килограммов (эквивалент силы приблизительно в 2450 ньютонов) на расстояние, равное 1 метру от точки опоры. Затем предположим, что на расстоянии 10 метров от точки опоры, с другой стороны рычага, человек прикладывает направленную вниз силу, равную 245 ньютонам (эквивалент веса в 25 килограммов). Крутящий момент, который создает эта сила (25∙10), равен и противоположен крутящему моменту, созданному весом с другой стороны рычага (250∙1). Рычаг находится в положении равновесия, и большой вес поддерживается малой силой. Если человек применит несколько большую силу (которая является все еще значительно меньшей, чем та, что создана весом с другой стороны), рычаг перевесит на его сторону.

Человек не столь чувствителен к крутящему моменту, как к силе (точнее, к мускульному усилию). Он знает, что не может создать достаточную силу, чтобы непосредственно поднять вес в 250 килограммов. Используя рычаг, однако, он может делать работу с силой, равной одной десятой той, которая потребовалась бы для прямого подъема. Регулируя длину рычага, он смог бы обойтись силой в одну сотую, в одну тысячную или в любую другую часть силы, действительно требуемой для прямого подъема. Полезность рычага как способа умножения сил человека для подъема грузов заложена в самом слове «рычаг» (lever), которое происходит от латинского слова, означающего «поднимать».

Без сомнения, еще первобытный человек наткнулся на этот «принцип рычага», но только во времена греческого математика Архимеда (ок. 287 — 212 до н.э.) ситуация впервые была проанализирована с научной точки зрения. Высокая оценка принципов использовании рычага отразилась в его знаменитой, хотя и немного напыщенной фразе: «Дайте мне точку опоры, и я переверну весь мир».

Любое устройство, которое передает силу от точки приложения к другой точке, где она используется, называется «механизмом» (machine — от латинского слова, означающего «изобретение» или «устройство»). Рычаг делает то, что сила, приложенная на одной стороне к точке опоры, может поднять вес с другой стороны; он делает это столь несложным способом, что далее упростить его уже невозможно. Поэтому рычаг является примером простого механизма. Другие примеры простых механизмов — наклонная плоскость, колесо и ось. Некоторые добавляют к этому списку еще три других простых механизма: шкив, клин и винт. Однако шкив может рассматриваться как своего рода рычаг, клин состоит из двух наклонных плоскостей, связанных основаниями, а винт представляет собой наклонную плоскость, «обвитую» вокруг оси.

Фактически все более сложные механизмы, изобретенные и используемые человечеством вплоть до недавнего времени, являются просто комбинациями двух или более простых механизмов. Эти механизмы зависят от движений и сил, вызванных действием в прямом контакте двигающихся тел. В результате та ветвь физики, которая имеет дело с такими движениями и силами, называется «механикой».

Та ветвь механики, которая имеет дело непосредственно с движением, называется «динамикой» (dynamics), в то время как та ветвь, что имеет дело с движениями, связанными с положением равновесия, называется «статикой» (statics — от греческого слова, означающего «остановить»). Архимед был первым великим ученым в области статики благодаря работам по изучению рычага. Галилео Галилей был первым великим ученым в области динамики.