Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Массу излучения нетрудно найти из оказываемого им давления при помощи следующих вычислений.

Давление солнечного луча на зеркало очень мало, но его можно измерить с помощью чувствительной «световой мельницы» в вакууме, а плотность энергии измеряется по нагреванию небольшого черного поглотителя. Измерения показывают:

[ДАВЛЕНИЕ СВЕТА на отражающее его зеркало] = [Удвоенная ПЛОТНОСТЬ ЭНЕРГИИ, равная (ЭНЕРГИЯ ПУЧКА)/(ЕГО ОБЪЕМ)]

Это согласуется с выводами законов электромагнетизма. Попробуем теперь получить давление из расчетов кинетической теории.

Пусть пучок света протяженностью а (фиг. 60) падает перпендикулярно на кусочек зеркала сечением b x d и отражается им Представим себе, что свет — это N упругих шариков массой m , летящих со скоростью с . Тогда время, необходимое для того, чтобы весь пучок попал на зеркало, будет а / с .

Фиг. 60. Радиационное давление.

Полное изменение количества движения равно N ∙2 mc , т. е.

СИЛА = ИЗМЕНЕНИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ / ВРЕМЯ =

= N∙2 mc/( a/ c) = 2∙ N∙ mc 2/ a,

или [172]

ДАВЛЕНИЕ = СИЛА/ bd= 2 Nmc 2/ abd= 2 mc 2/ОБЪЕМ

Сравним это с экспериментом. Тогда

2∙(ЭНЕРГИЯ)/ОБЪЕМ = 2∙ Мс 2/ОБЪЕМ

т. е. энергия пучка света равна Mс 2, или M= E/ с 2.

Таким образом, излучение, подобно потоку шариков, обладает массой, равной E / с 2. Это не строгое доказательство, а некое возможное истолкование экспериментальных следствий. Гораздо лучший вывод дан в конце гл. 31 .

Формула E= mc 2напоминает выражение E= 1/ 2 Mv 2. Поскольку мы имеем дело с излучением, то v должно замениться на с . Но куда делась 1/ 2? Причина в том, что формула 1/ 2 Mv 2дает неточное выражение для кинетической энергии. Оно справедливо для обычных скоростей, а для больших скоростей, близких к с , теория относительности дает другое выражение, о котором будет сказано в следующем разделе [173].

Излучение имеет массу Е / с 2? При испускании излучения источник испытывает отдачу и мы заключаем, что он теряет массу Е / с 2. При поглощении излучения приемник должен приобретать дополнительную массу Е / с 2. Так что к излучению и его взаимодействию с веществом применим закон Е= М∙ с 2. А можно ли его обобщить и всем формам энергии приписать массу Е / с 2? Теория относительности отвечает утвердительно.

2) Теория относительности

Стремление увязать воедино серию экспериментальных парадоксов, касающихся абсолютного пространства и времени, породило теорию относительности. Два сорта экспериментов со светом давали противоречивые результаты, а опыты с электричеством еще больше обострили этот конфликт. Тогда Эйнштейн предложил изменить простые геометрические правила сложения векторов. Это изменение и составляет сущность его «специальной теории относительности». Более детальному обсуждению ее посвящена гл. 31 . Теперь же мы примем эйнштейновскую схему обращения с длинами, временем, скоростями и другими векторами. После этого конфликты исчезнут, а экспериментальные результаты и общие законы уложатся в единую схему.

Для малых скоростей (от медлительной улитки до быстрейшей из ракет) новая теория согласуется со старой: кинетическая энергия равна 1/ 2 Mv 2, а вещество сохраняет постоянную массу независимо от того, движется оно или нет. При высоких скоростях, сравнимых со скоростью света, наше измерение длин или времени модифицируется движением тела относительно наблюдателя, в частности масса тела становится тем больше, чем быстрее оно движется. Эйнштейн показал, что для тела, движущегося мимо нас со скоростью v , вместо правила m= const , нужно пользоваться формулой m= ( постоянная )/√(1 — ( v 2/ c 2)), где с — скорость света.

Входящую сюда постоянную мы называем «массой покоя» тела, m 0. После этого эйнштейновская формула принимает вид m= m 0/√(1 — ( v 2/ c 2)). Теория электричества уже использовала этот закон для «массы» движущихся электрических зарядов, а эксперименты с электронами высоких скоростей подтвердили его. Затем теория относительности провозгласила, что это увеличение массы носит совершенно общий характер. При обычных скоростях никаких изменений нет и только при скорости 100 000 000 км/час масса возрастает на 1 %. Однако для электронов и протонов, вылетающих из радиоактивных атомов или современных ускорителей, оно достигает 10, 100, 1000 %…. Опыты с такими высокоэнергетическими частицами великолепно подтверждают соотношение между массой и скоростью.

Любая обычная скорость настолько мала по сравнению с с , что отношение v / c будет очень мало, а v 2/ c 2— и того меньше. Следовательно, √(1 — ( v 2/ c 2)) практически равно единице. При малых скоростях масса оказывается постоянной, m= m 0/1.

Затем, приняв ньютоновское определение силы F= Δ( mv)/Δ tи измеряя работу произведением F ∙Δ s , Эйнштейн показал, что кинетическая энергия любого движущегося тела равна ( m — m 0)∙ с 2. Поскольку ( m — m 0) — это приращение массы вследствие движения, то E кин= ( приращение массы )∙ с 2. Это и есть соотношение Е= mc 2 для кинетической энергии и ее массы . Добавляя сюда постоянный запас энергии, заключенный в массе, m 0 с 2, Эйнштейн нашел, что

ПОЛНАЯ ЭНЕРГИЯ = ( m — m 0)∙ с 2+ m 0 с 2= mс 2.

(Более детально эти вопросы будут обсуждаться в гл. 31 , но даже там мы не дадим вывода, ибо он требует высшей математики.)

Формула E кин= ( m — m 0)∙ с 2выглядит совсем по-другому, чем E кин= 1/ 2 mv 2. Они действительно отличаются, как и должно быть. Но посмотрите на эту величину при малых скоростях. Предположим, что v мало по сравнению с с , так что и v 2/ c 2мало по сравнению с единицей. Затем, пользуясь теоремой о биноме (см. гл. 22 , примечание на стр. 239), получаем

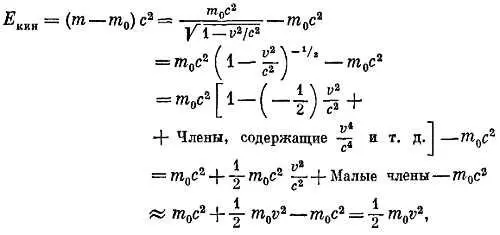
т. е. старое выражение для кинетической энергии. Вот как работает хорошая теория, воспроизводя в предельном случае старый результат и указывая на его ограничение — малые скорости.

Мы говорим, что дополнительная масса движущегося тела — это масса [174]его кинетической энергии. Тело с массой покоя т0 при любой скорости обладает массой m 0+ ( E кин/ c 2), как это нетрудно увидеть из вида кинетической энергии в теории относительности. При малых скоростях биномиальное приближение дает