Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

Проверка закона Кулона

ДЕМОНСТРАЦИОННЫЙ ОПЫТ

Можно приближенно произвести непосредственную проверку закона Кулона, измерив силу взаимодействия между двумя зарядами. Мы сообщаем большой заряд двум металлическим шарикам [50]и «взвешиваем» один шарик, когда второй удален от него на 0,1, 0,2, 0,3 м и т. д., считая расстояние между центрами.

Вам следовало бы посмотреть, как проделывается описываемый опыт, пусть это будут лишь грубые измерения, чтобы воочию убедиться в справедливости этого замечательного экспериментального закона. В задаче 7 приведен пример записи результатов измерений, позволяющий получить представление об этом опыте в том случае, если вам не удастся его посмотреть.

Задача 7. Проверка закона Кулона (фиг. 69)

Шарик А прикреплен к одному концу плексигласового коромысла. Слабая (но хорошая) стальная пружина уравновешивает вес шарика и позволяет измерить любую дополнительно действующую на шарик силу. У второго конца коромысла укреплена длинная стрелка, против которой расположена вертикальная шкала. Шарик В крепится отдельно на подвижном изолирующем стержне над шариком А . От стержня, на котором крепится шарик В , вниз отходит стержень из плексигласа с делениями, позволяющий измерить расстояние между шариками. Каждый шарик был заряжен с помощью электрофора. Шарик В относили на большое расстояние и устанавливали стрелку, связанную с шариком А , против нуля шкалы. Затем шарик В располагали над А на определенном расстоянии по вертикали и отсчитывали показание стрелки, по которому можно оценить силу отталкивания. (Шкала разбита на произвольные деления, каждое примерно по 1 см. Чтобы оценить жесткость пружины — нам она здесь не нужна, — на шарик А помещали груз 1 г; при этом отсчет по шкале равен 49.) Ниже в таблице приведена для примера запись результатов измерений («бесконечность» означает, что шарик В убран).

а) Перепишите таблицу, добавив столбец ДЛЯ ПРОВЕРКИ ЗАКОНА КУЛОНА. Проделайте вычисления с целью проверить обратную пропорциональность квадрату расстояния.

б) Предполагая, что значение 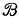(которое мы измерим позже) равно 9,0∙10 9, и считая оба заряда равными, оцените их величину в кулонах. (Обратите внимание на то, что сила должна быть выражена в ньютонах.)

Фиг. 69. Проверка закона обратной пропорциональности квадрату расстояния.

Электрические поля

Мы представляем себе, что с каждым зарядом связано электрическое поле, подобное в известном смысле полю тяготения. Напряженность электрического поля в любой точке определяют как силу, действующую на пробный кулон, помещенный в эту точку . Принимая во внимание, что 1 кулон — огромный заряд, сформулируем это определение более реалистически следующим образом:

НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ = СИЛА, ДЕЙСТВУЮЩАЯ НА МАЛЫЙ ПРОБНЫЙ ЗАРЯД / ВЕЛИЧИНА ПРОБНОГО ЗАРЯДА

Мы получаем силу, действующую на единичный заряд, в ньютон / кулон [51].

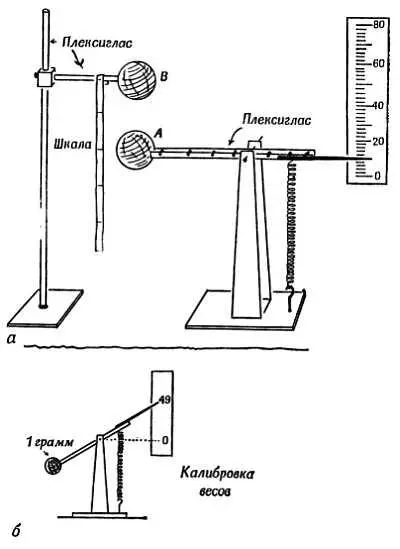
На фиг. 70 показаны «демоны», занятые экспериментальным исследованием напряженности поля тяготения и электрического поля.

Фиг. 70. Измерение напряженности поля.

аи б— измерение напряженности гравитационного поля Земли; сила притяжения эталона килограмма измеряется в ньютонах; в— измерение напряженности электрического поля; г— «измеритель напряженности электрического поля».

Чтобы избежать искажения измеряемого поля и не иметь дела при измерениях с огромными силами, пробный заряд должен быть значительно меньше, чем 1 кулон . Тогда мы должны будем измерять силу, действующую, скажем, на заряд в 1 миллиардную кулона, с помощью пружинных весов, проградуированных в миллиардных долях ньютона. При этом мы определим напряженность поля в ньютон / кулон .

Напряженность поля вокруг малого изолированного заряда изменяется обратно пропорционально квадрату расстояния.

НАПРЯЖЕННОСТЬ ПОЛЯ = СИЛА, ДЕЙСТВУЮЩАЯ НА ПРОБНЫЙ ЗАРЯД / ПРОБНЫЙ ЗАРЯД =

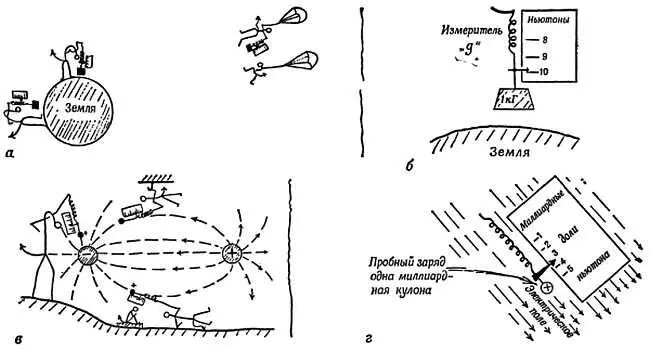
То же самое справедливо для изолированного заряженного шара. Напряженность поля — вектор. Кроме величины, поле характеризуется направлением силы, действующей на положительный пробный заряд. Можно начертить карту направлений электрического поля с помощью воздушного шарика, реального или воображаемого, несущего малый пробный заряд. На фиг. 71 показаны два громадных металлических шара, заряженных положительно и отрицательно. Заряженный воздушный шарик будет перемещаться от одного шара к другому вдоль любой из траекторий, показанных пунктирными линиями. Они называются силовыми линиями . Эти линии указывают направление поля, т. е. направление результирующей силы, действующей на пробный заряд.

Фиг. 71. Определение конфигурации электрического поля.

Путем геометрического построения находят последовательно в разных точках направление результирующей силы, приложенной к пробному заряду.

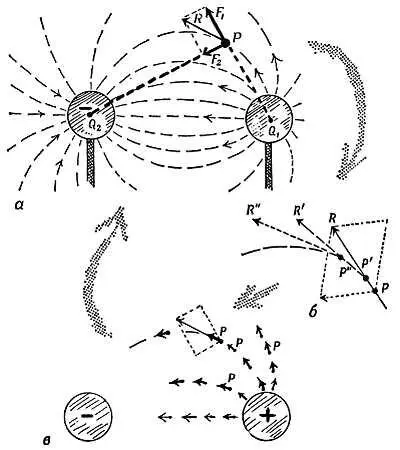
Силовые линии искривлены потому, что на пробный заряд действуют силы отталкивания со стороны одного заряда, + Q 1, и силы притяжения со стороны другого заряда, — Q 2, которые изменяются по направлению и по величине от точки к точке. Пользуясь правилом сложения векторов, можно найти конфигурацию силовых линий в подобных случаях, хотя это связано с утомительной процедурой. Предположим, два заряда, создающие поле, равны и противоположны по знаку. Пробный заряд q , помещенный в точку Р , испытывает силу отталкивания F 1со стороны заряда Q 1и меньшую силу притяжения F 2со стороны заряда Q 2(меньшую потому, что Q 2дальше). Сложение этих сил дает результирующую силу R , действующую на q . В точке Р силовая линия поля направлена вдоль R . Повторим теперь это рассмотрение для другой, соседней точки Р ' затем для точки Р " и т. д. Точка Р ' выбрана на малом расстоянии от Р , отсчитанном практически вдоль силы R (которая указывает направление поля в Р ), точка Р " взята на R '. Можно затем объединить эти построения и получить часть силовой линии. Существуют методы, приводящие к цели быстрее. В них используются более сложные геометрические представления, но в основе лежит тот же закон обратной пропорциональности квадрату расстояния. Эти методы дают целую сетку силовых линий и позволяют определить картину силовых линий других полей, например, показанных на фиг. 72.