Брайан Кокс - Почему Е=mc²? И почему это должно нас волновать

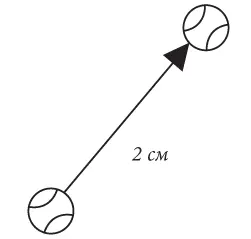
Рис. 11

Нам удалось построить вектор импульса шара в трехмерном пространстве, хотя вряд ли это можно назвать самым увлекательным из всего, что мы сделали. Теперь предпримем смелый шаг и попытаемся построить вектор импульса в пространстве-времени, причем осуществим это точно таким же способом, что и в трехмерном пространстве. Единственное ограничение – мы будем использовать только те объекты, которые носят универсальный характер в пространстве-времени.

Снова начнем со стрелки, на этот раз указывающей направление в четырехмерном пространстве, как видно на рис. 12. Один ее конец показывает, где находится наш шар в начальный момент времени, а другой – где он будет через какое-то время. Длину стрелки необходимо определять по формуле Минковского для расчета расстояния в пространстве-времени, а значит, она задается уравнением (∆ s )2 = ( c ∆ t )2 – (∆ x )2. Вспомните, что ∆ s – это длина, с которой будут согласны все без исключения (то, что ни в коем случае нельзя сказать ни о ∆ x , ни о ∆ t по отдельности), а значит, именно это расстояние мы должны использовать вместо расстояния ∆ x , представленного в определении импульса в трехмерном пространстве. Но чем заменить интервал времени ∆ t ? (Не забывайте: мы пытаемся найти замену m ∆ x/ ∆ t в четырехмерном пространстве.) Проблема в том, что мы не можем использовать ∆ t , поскольку эта величина не инвариантна в пространстве-времени. Как мы неоднократно подчеркивали, интервалы времени для разных наблюдателей различны, а значит, мы не должны использовать временн ы е интервалы в определении четырехмерного импульса. Но какие у нас есть варианты? На что мы могли бы разделить длину стрелки, чтобы вычислить скорость движения шара в пространстве-времени?

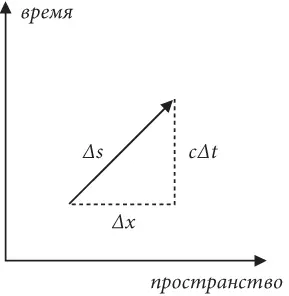
Рис. 12

Нам необходимо вывести нечто более совершенное, чем старый трехмерный импульс, а также убедиться, что если мы имеем дело с объектами, движущимися со скоростью, которая гораздо меньше скорости света, то новый импульс приблизительно эквивалентен старому. С учетом этого требования мы должны разделить длину нашей стрелки в пространстве-времени ∆ s на величину того же типа, что и интервал времени. В противном случае новый четырехмерный импульс будет представлять собой нечто абсолютно иное по сравнению со старым трехмерным импульсом. Промежутки времени можно измерять в секундах, значит, нам следует получить некую величину, которую тоже можно было бы измерять в секундах. Учитывая инвариантные величины в пространстве-времени, скорость света c и расстояние ∆ s , есть только один возможный вариант: число, полученное посредством деления длины стрелки (∆ s ) на скорость c . Другими словами, если ∆ s измеряется в метрах, а скорость c – в метрах в секунду, то ∆ s/c – в секундах. Это и должно быть то число, на которое нам необходимо разделить длину стрелки, поскольку это единственная имеющаяся в нашем распоряжении инвариантная величина, измеряемая в требуемых единицах, – время. Давайте пойдем дальше и разделим ∆ s на время ∆ s/c . В результате получим просто c (по той же причине, что и в случае, когда результат деления единицы на ½ равен двум). Другими словами, четырехмерный аналог скорости в нашей формуле трехмерного импульса – это такой универсальный показатель, как предельная космическая скорость c .

Все это может показаться вам знакомым, но только потому, что так и должно быть. Мы лишь рассчитали скорость объекта (в нашем примере шара) в пространстве-времени и получили в итоге c . Но мы уже приходили к аналогичному выводу в предыдущей главе, когда анализировали движение мотоциклиста по равнине пространства-времени. В контексте данной главы мы добились большего, поскольку пришли к выводу, что вектор скорости в пространстве-времени можно использовать также в новом определении четырехмерного импульса. Вектор скорости объекта, движущегося в пространстве-времени, всегда имеет протяженность c и всегда указывает в пространстве-времени в направлении движения объекта.

Все, что нам необходимо сделать, для того чтобы завершить построение нового вектора импульса в пространстве-времени, – это умножить вектор скорости в пространстве-времени на массу m . Из этого следует, что наш предполагаемый вектор импульса всегда имеет длину, равную mc , и указывает в направлении движения объекта в пространстве-времени. На первый взгляд этот новый вектор импульса немного скучноват, поскольку его длина в пространстве-времени неизменна. Создается впечатление, что наше начало вряд ли можно назвать удачным. Однако мы не должны останавливаться. Нам еще предстоит выяснить, существует ли взаимосвязь между вектором импульса в пространстве-времени, который мы только что построили, и устаревшим трехмерным вектором, или, если уж на то пошло, пригодится ли он нам в новом мире пространства-времени.

Для того чтобы углубиться в ситуацию, давайте посмотрим на те части нашего нового вектора импульса в пространстве-времени, которые указывают направление в пространстве и времени по отдельности. Увы, здесь нам не обойтись без математики. Приносим извинения читателям, не владеющим глубокими математическими знаниями, и обещаем продвигаться очень медленно. Помните: у вас всегда есть возможность бегло просмотреть уравнения и перейти к заключительным выводам. Математика делает приведенные здесь доводы более убедительными, но вы вполне можете продолжать чтение, не углубляясь в детали. Точно так же хотим извиниться и перед читателями, знакомыми с математикой, за слишком подробное изложение материала. Но ведь нельзя угодить всем сразу!

Ранее мы с вами вывели выражение для длины вектора импульса в трехмерном пространстве – m ∆ x/ ∆ t . Мы исходили из того, что ∆ x следует заменить на ∆ s , а ∆ t – на ∆ s/c , для того чтобы получить четырехмерный вектор импульса, который имеет на первый взгляд неинтересную длину mc . Потерпите нас еще один абзац и позвольте написать замену для ∆ t , то есть для ∆ s/c , в полном виде: ∆ s/c равно √(( c ∆ t )² − (∆ x )²) ÷ c . Это несколько громоздкое выражение, однако небольшая математическая манипуляция позволяет записать его в более простом виде: ∆ t/ γ, где γ = 1 ÷ √(1 − v ² ÷ c²). Для получения этой формулы мы использовали тот факт, что скорость объекта рассчитывается как v = ∆ x/ ∆ t . В таком случае γ – это не что иное, как множитель, о котором шла речь в главе 3, выражающий величину замедления времени с точки зрения того, кто наблюдает за быстро пролетающими мимо часами.