Брайан Кокс - Почему Е=mc²? И почему это должно нас волновать

Мы установили, что значение γ mc должно сохраняться. Теперь нам необходимо объяснить, что именно это означает. Если вы представите себе игру в релятивистский бильярд, то в ней каждый шар имеет свое значение γ mc . Сложите вместе все эти значения – и какой бы ни была общая сумма, она останется неизменной. А теперь давайте поиграем в игру, которая поначалу покажется бессмысленной. Если значение γ mc сохраняется, то сохраняется и значение γ mc ² – просто потому, что c – это константа. Вскоре вам станет понятно, зачем мы так поступили. В то же время значение γ не равно в точности единице, и в случае малых скоростей его можно аппроксимировать посредством формулы γ = 1 + v ² ÷ 2 c ². С помощью калькулятора вы можете проверить самостоятельно, что эта формула работает достаточно хорошо для скоростей, которые можно считать малыми по сравнению с с (то есть она дает практически те же значения, что и точная формула γ = 1 ÷ √(1 − v ²/ с ²). Если у вас под рукой нет калькулятора, надеемся, представленная ниже таблица вас убедит. Обратите внимание, что приближенная формула (которая дает значения, представленные в третьем столбце) на самом деле очень точна даже в случае скоростей, составляющих десять процентов от скорости света ( v / c = 0,1), что представляет собой недостижимую в обычных условиях скорость 30 миллионов метров в секунду.

Таблица

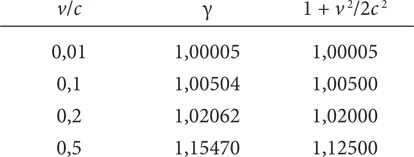
Если принять это упрощение, то значение γ mc ² приближенно равно mc ² + ½ mv ². В этот момент мы можем осознать крайне важные последствия наших действий. Мы пришли к выводу, что для малых по сравнению с с скоростей сохраняется величина mc ² + ½ mv ². Точнее говоря, величина γ mc ², но на данном этапе первое уравнение гораздо лучше позволяет понять суть происходящего. Почему? Как вы уже знаете, произведение mv ² ÷ 2 – это кинетическая энергия, с которой мы познакомились в примере со сталкивающимися бильярдными шарами. Благодаря этой формуле можно определить, какой энергией обладает объект с массой m , движущийся со скоростью v . Мы обнаружили, что существует нечто сохраняющееся, равное чему-то ( mc ²) плюс кинетическая энергия. Имеет смысл называть это «нечто» сохраняющейся энергией, но у него есть две составляющие: одна – mv ² ÷ 2 и вторая – mc ². Пусть вас не сбивает с толку тот факт, что мы выполнили умножение на с . Мы сделали это исключительно для того, чтобы наш окончательный ответ включал в себя такой член уравнения, как mv ² ÷ 2, а не mv ² ÷ 2 с. Первая из двух формул описывает то, что ученые многих поколений называли кинетической энергией. При желании вы можете обозначить mv ² ÷ 2 с термином «кинетическая масса» или придумать любое другое название, которое здесь не играет особой роли (даже если оно столь же важное, как термин «энергия»). Имеет значение лишь следующее: временн а я компонента вектора момента в пространстве-времени и эта величина сохраняются. Нужно признать, что формулировка «временн а я компонента вектора момента в пространстве-времени равна mc » выглядит не столь привлекательно, как E = mc² , но их физика одинакова.

Мы продемонстрировали, что сохранение импульса в пространстве-времени приводит не только к появлению новой, усовершенствованной версии закона сохранения импульса в трехмерном пространстве, но и к пересмотру закона сохранения энергии. Давайте представим себе систему движущихся частиц. Как мы уже говорили выше, сумма их кинетических энергий плюс масса всех частиц, умноженная на квадрат с , дает нам некую неизменную величину. Ученые викторианской эпохи были бы очень довольны утверждением, что сумма кинетических энергий должна оставаться неизменной. Кроме того, их порадовало бы и утверждение, что сумма масс также не должна изменяться (умножение на с не играет особой роли, когда речь идет о чем-то неизменном). Наш новый закон соответствует действительности, но это далеко не все. При таком положении вещей ничто не мешает какой-то части массы превращаться в кинетическую энергию и наоборот при условии, что сумма этих двух вещей не меняется. Мы обнаружили, что масса и энергия взаимозаменяемы, а количество энергии, которую можно извлечь из массы m , находящейся в состоянии покоя (γ в этом случае равно единице), определяется уравнением E = mc² .

Давайте подведем итог. Мы хотели найти в пространстве-времени объект, который выполнял бы те же функции, что и импульс в трехмерном пространстве, поскольку импульс полезен тем, что представляет собой сохраняющуюся величину. Мы смогли отыскать такой объект, только составив его из тех элементов, по поводу значения которых все наблюдатели приходят к согласию, а именно расстояние в пространстве-времени, универсальная предельная космическая скорость и масса. Построенный нами вектор импульса в пространстве-времени оказался очень интересным. Проанализировав ту его часть, которая указывает направление в пространстве, мы обнаружили все тот же закон сохранения импульса с небольшой поправкой: в пространстве-времени он распространяется на объекты, которые движутся со скоростью, близкой к скорости света. Но самое ценное открытие было сделано в процессе изучения части вектора, указывающей в направлении времени. Мы получили совершенно новую версию закона сохранения энергии. Старая кинетическая энергия mv ² ÷ 2 все еще присутствует в этой версии закона, но появилась еще одна, абсолютно новая составляющая – mc ². Таким образом, даже если объект не двигается, он обладает энергией и она определяется знаменитым уравнением Эйнштейна E = mc² .

Что все это означает? Мы установили, что энергия представляет для нас интерес, поскольку сохраняется: количество энергии в одном месте может увеличиться, только если ее количество в другом месте уменьшится. Кроме того, мы пришли к выводу, что сама масса объекта – потенциальный источник энергии. Представим себе, как берем сгусток материи, скажем, килограмм вещества (не имеет значения, какого именно), и делаем с ним нечто такое, после чего этот килограмм исчезает, то есть не разлетается на крохотные кусочки, а именно исчезает. Совсем. Мы можем нарисовать себе крайний вариант развития событий, при котором используется вся исходная масса вещества. На ее месте должна появиться энергия, количество которой эквивалентно килограмму вещества (плюс энергия, которую мы вложили в манипуляции с этим веществом). Она может быть в форме массы. Например, может быть создано несколько граммов нового вещества, а оставшаяся энергия будет выражена в форме кинетической энергии: это новое вещество может очень быстро двигаться. Разумеется, это не более чем воображаемый сценарий – мы просто все это придумали. Однако следует по достоинству оценить тот факт, что, согласно теории Эйнштейна, все это могло бы произойти. До Эйнштейна никто даже не мечтал разрушить массу и преобразовать ее в энергию, поскольку считалось, что масса и энергия – совершенно не связанные друг с другом сущности. После Эйнштейна всем пришлось признать тот факт, что масса и энергия – разные проявления одной и той же сущности. Дело в том, что, как мы открыли, энергия, масса и импульс образуют в совокупности единый пространственно-временной объект, который мы назвали вектором импульса в пространстве-времени. На самом деле физики чаще обозначают его термином «четырехмерный вектор энергии-импульса». Раньше мы с вами узнали, что пространство и время не следует рассматривать как две отдельные сущности. Точно так же теперь мы обнаружили, что энергия и импульс – это составляющие более сложного объекта, четырехмерного вектора энергии-импульса. Мы ошибочно считаем их не связанными друг с другом, отличающимися друг от друга понятиями, что объясняется нашим предвзятым интуитивным стремлением проводить различие между пространством и временем. Важно отметить, что природа использует этот шанс – превратить массу в энергию все же можно. Если бы природа сделала это невозможным, мы даже не появились бы на свет.