Николя Жизан - Квантовая случайность. Нелокальность, телепортация и другие квантовые чудеса

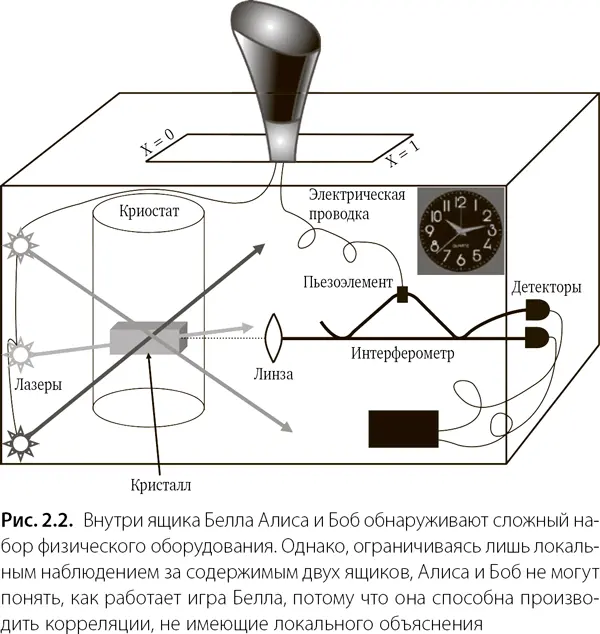
Но обследование приборов не дает нам ясности, и в этом основной посыл этой главы. Просто исследуя устройство приборов и то, как они работают, даже с максимальной детализацией, мы никогда не найдем удовлетворительного объяснения. В любом случае мы уже знаем, что не существует локального объяснения для победы в игре Белла, поэтому мы никак не найдем его, заглядывая локально под крышку каждого из приборов! Вернемся немного назад. В конце концов, все это сложное оборудование служит лишь для того, чтобы выдать нам двоичный результат каждый раз, когда джойстик наклонен вправо или влево. Следовательно, даже если механизм очень сложен, все, на что устройство способно, это выводить результат одной из четырех программ, описанных выше. А что еще оно может делать-то? Еще раз повторю, что есть только два возможных положения джойстика и только один двоичный результат. Использование нескольких лазеров, криостата и детекторов фотонов кажется избыточным для выполнения такой простой программы. Но эта установка делает больше, ведь она помогает нам выиграть!

Физик доквантовой эпохи потратил бы много времени на изучение приборов и все равно ничего не понял бы, поэтому читатель не должен стыдиться, что тоже не понимает, что происходит внутри. Мы узнаем решение в главе 6, а пока отметим только, что главными элементами наших приборов являются кристаллы, и эти кристаллы запутаны [18] Для специалистов мы должны уточнить, что не весь кристалл Алисы запутан с кристаллом Боба. Каждый из кристаллов состоит из нескольких миллиардов ионов редкоземельных элементов. Несколько коллективных возбуждений этих ионов в кристалле Алисы запутано с аналогичным возбуждением ионов в кристалле Боба. (Christoph Clausen, Imam Usmani, Félix Bussières, Nicolas Sangouard, Mikael Afzelius, Hugues de Riedmatten, and Nicolas Gisin: Quantum storage of photonic entanglement in a crystal, Nature 469, 508–511, January 2011.) . Но что это значит? Пока «запутанность» – это лишь слово, которое мы используем как имя для концепции квантовой физики, которая позволяет нам победить в игре Белла. Будем же терпеливы!

В итоге нам не так важно, что именно находится в приборах. Важно лишь то, что физики знают – в принципе, как построить приборы, которые позволят Алисе и Бобу выиграть в более чем трех случаях из четырех, и что главный ингредиент проходит под именем «запутанность».

Сама возможность победы в игре Белла – это уже значительный вывод, такой же ослепительно ясный, как фотография Земли в пустоте космоса: Земля круглая, а квантовая физика предсказывает нелокальные корреляции.

Мы уже знаем, что довольно просто получить в игре Белла счет 3. К примеру, достаточно заранее договориться каждый раз выдавать один и тот же результат. Но мы также видели, что нельзя указать никакую локальную стратегию, применяя которую независимо друг от друга, Алиса и Боб могли бы выигрывать чаще, чем три раза из четырех. Это было основным выводом главы 2.

Но если два игрока действительно побеждают, то есть получают более 3 очков из четырех, какой вывод мы обязаны сделать? Первое и самое очевидное заключение сводится к двум вариантам: либо они воздействуют друг на друга каким-то неуловимым образом, либо каким-то образом жульничают. Но предположим, что в наших силах исключить эти две возможности. Тогда можно допустить, что мы ошиблись в умозаключениях, представленных в главе 2. Многие физики и философы потратили годы на изучение этого. Почему бы и вам не потратить на это несколько минут? Помните, что никогда нельзя принимать доводы на веру. У каждого есть право и долг проверять научные рассуждения самому. Очень важно, что доказательство невозможности выиграть в игру Белла без коммуникации очень простое и ясное. Действительно, каждый из двух игроков может выбрать только одну из четырех возможных стратегий. Таким образом, есть всего лишь 4 × 4 = 16 возможных комбинаций стратегий и ни одна из них не дает возможности выигрывать чаще, чем три раза из четырех (см. таблицу 2.1 в главе 2). Просмотрите доказательство еще раз и попробуйте объяснить его приятелю.

Есть все основания быть уверенным в бесспорности этого доказательства. Оно совершенно надежно и проверено тысячами физиков, философов, математиков и специалистов по информатике и вычислительной технике. Но зачем тогда вообще обсуждать проблему выигрыша со счетом больше, чем три из четырех, если это считается невозможным? Это действительно жгучий вопрос. Доказательство настолько просто, что, если бы не квантовая физика, никому не было бы до него дела. Оно так и оставалось бы очевидным фактом среди кучи других неинтересных очевидных фактов, не применимых ни к чему стоящему. Есть единственная причина приглядеться к этому вопросу: дело в том, что современная физика может выиграть в эту игру, даже если игроки не обмениваются информацией и не жульничают.

Вернемся к нашему вопросу: какой вывод мы можем сделать из того, что кто-то систематически выигрывает в игру Белла более, чем 3 раза из 4? Единственная возможность такова: приборы Алисы и Боба, хотя они и разделены пространственно, не разделены логически. Несмотря на расстояние между ними, мы не можем описать ящик Алисы на одной стороне и ящик Боба на другой как отдельные сущности. Другими словами, мы не можем просто сказать, что делает прибор Алисы с одной стороны и что делает прибор Боба с другой. Все происходит так, как будто, несмотря на расстояние между ними, приборы действуют как одна сущность, которую нельзя логически разделить на две части. Короче говоря, они составляют нелокальное целое.

Но что такое нелокальное целое? Теперь вам стало понятнее? Скорее всего нет, только если вы не гений! Здесь слово «нелокальное» означает нечто, которое не может быть описано как две независимых и хорошо локализованных части. Конечно, Алиса и Боб со своими ящиками хорошо локализованы, как любые нормальные люди или ящики. Мы можем окружить их железобетонными стенами и покрыть свинцовой оболочкой или принять другие подобные меры, но мы не сможем описать их поведение отдельно друг от друга: вот так себя ведет прибор Алисы, а вот этак – прибор Боба. В самом деле, если бы каждый из них имел собственное поведение и, следовательно, руководствовался бы своей стратегией, выиграть в игру Белла было бы невозможно. И это утверждение остается справедливым, даже если стратегии и поведение оговорены и скоординированы заранее, еще до того, как приборы разнесли в пространстве.

И здесь мы подходим к замечательному выводу, который не так просто переварить. Если Алиса и Боб завершают игру со счетом более чем 3 из 4, мы вынуждены признать, что, несмотря на расстояние между ними и возможность идентифицировать двух игроков, такой результат их игры не может быть получен локально, отдельно на приборе Алисы и отдельно на приборе Боба. Эти результаты получаются нелокальным образом . Все происходит так, как будто прибор Алисы «знает» что делает прибор Боба, и наоборот.