Николя Жизан - Квантовая случайность. Нелокальность, телепортация и другие квантовые чудеса

1. a = 0, вне зависимости от значения x .

2. a = 1, вне зависимости от значения x .

3. Значение результата идентично значению выбора, то есть a = x .

4. Значение результата всегда отличается от значения выбора, то есть a = 1 − x .

То же самое справедливо для прибора Боба. Это означает, что общее количество комбинаций программ для обоих приборов равно: 4 × 4 = 16. Конечно, программа Алисы, как и программа Боба, может меняться от минуты к минуте, но для каждой конкретной минуты одна из четырех программ в ящике Алисы определяет результат а и одна из четырех программ в приборе Боба определяет результат b .

Давайте изучим эти 16 возможных комбинаций и рассчитаем соответствующие им результаты игры. Помните, что наша цель – найти максимально возможный счет в рамках локального объяснения. Мы увидим, что невозможно создать аппараты, использующие локальные стратегии, которые бы давали счет больше 3. Вы можете принять мои слова на веру и сразу перейти к странице разделу «Победить в игре Белла: нелокальные корреляции» или убедиться в этом самостоятельно, потратив время на рассуждения в следующем абзаце. И я настоятельно рекомендую сделать именно так.

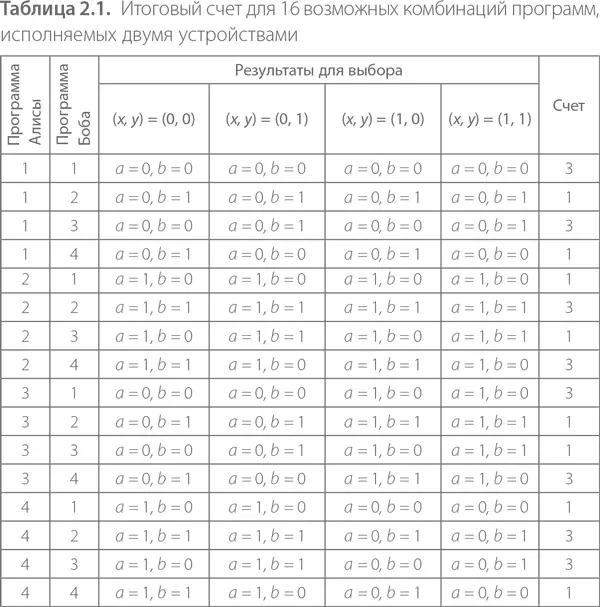
Начнем с сочетания программы № 1 для Алисы и программы № 1 для Боба. В этом случае оба результата всегда будут равны 0, то есть a = b = 0, и Алиса и Боб выигрывают три раза из четырех. В самом деле, они проигрывают лишь в том случае когда оба выбирают 1. Возьмем второе сочетание, скажем программу № 1 для Алисы (и поэтому всегда a = 0) и программу № 3 для Боба (поэтому b = y ). Рассмотрим четыре пары возможных выборов, которые они могут сделать. При x = 0 и y = 0 значение результата будет (0, 0), и Алиса и Боб выигрывают – в смысле зарабатывают очко. При x = 0 и y = 1 участники проигрывают, так как результат будет (0, 1). При x = 1 и y = 0 результатом является (0, 0), значит, Алиса и Боб выигрывают. И наконец, при x = 1 и y = 1 значение результата будет (0, 1), что снова означает выигрыш, ведь при x = y = 1 цель состоит в том, чтобы получить разные результаты. Суммируем и получаем, что Алиса и Боб снова заработают 3 очка.

Теперь вы можете самостоятельно завершить доказательство для оставшихся 14 комбинаций вариантов программ. Или просмотреть готовые результаты, представленные в таблице 2.1.

Подведем итог. Какова бы ни была локальная стратегия создателя ящиков и какова бы ни была вследствие этого комбинация программ, Алиса и Боб никогда не смогут выиграть игру Белла более трех раз из четырех возможных. Физики предпочитают выражать это в виде неравенства. Оно называется неравенством Белла [13] Точнее, это самое простое из семейства неравенств Белла, эквивалентное неравенству CHSH, которое было названо по первым буквам фамилий его первооткрывателей: J. F. Clauser, M. A. Horne, A. Shimony, R. A. Holt: Proposed experiment to test local hidden-variable theories , Phys. Rev. Lett. 23 , 880 (1969). Другие неравенства описывают случаи с большим количеством вариантов выбора, возможных результатов или большим количеством игроков. . Учитывая, что это неравенство самым прямым образом относится к теме книги, я выпишу его здесь. Если даже вы не сможете полностью уяснить его значение, попытайтесь оценить его восхитительное изящество, в чем-то похожее на красоту музыкальной партитуры:

Выражение P ( a = b | x, y ) читается следующим образом: вероятность того, что a равно b , при условии, что сделан определенный выбор x и y . Выражение P ( a ≠ b |1, 1) читается так: вероятность того, что a отличается от b , при сделанном выборе x = y = 1. Неравенство Белла утверждает как раз то, что мы только что обнаружили, а именно что сумма всех четырех вероятностей в игре Белла, которая дает счет игры, не может быть больше 3. Для локальных корреляций неравенство Белла всегда удовлетворяется.

Справка 3.Неравенство Белла. В общем смысле вероятность P ( a, b | x, y ) возникает из статистической смеси различных возможных ситуаций. К примеру, первая возможная ситуация, традиционно обозначаемая λ1, может произойти с вероятностью ρ (λ1), вторая возможная ситуация λ2 – с вероятностью ρ (λ2) и так далее. Эти вероятности ρ (λ) также могут использоваться для анализа в случаях, когда мы не знаем точно реальную ситуацию. На самом деле нам даже не нужно знать вероятность наступления конкретной ситуации. Достаточно знать, что разные ситуации возникают с разной вероятностью.

Эти ситуации λ могут включать квантово-механическое состояние системы, обычно обозначаемое как ψ. То есть они могут включать всю прошлую жизнь Алисы и Боба или даже состояние всей вселенной, кроме одного – выбор x и y должен быть независим от λ. С другой стороны, λ может быть очень и очень ограничено, подобно выбору стратегий Алисы и Боба в игре Белла. Когда-то λ назвали локальными скрытыми переменными, но лучше рассматривать их как физическое состояние систем (к примеру, ящиков Алисы и Боба), описываемое любой современной или будущей теорией. Итак, неравенства Белла что-то сообщают нам о структуре любой будущей физической теории, совместимой с сегодняшними экспериментами. При этом единственное допущение относительно λ состоит в том, что они не содержат информации о выборе x и y.

Для каждой ситуации λ условная вероятность всегда может быть выражена как

Предположение о локальности позволяет утверждать, что для любой λ происходящее в приборе Алисы не зависит от происходящего в приборе Боба, что выражается как P ( a | x , y, λ) = P ( a | x , λ) и наоборот: P ( b | x , y, a , λ) = P ( b |y, λ).

В итоге допущение, лежащее в основе всех неравенств Белла, может быть найдено путем усреднения по всем возможным ситуациям λ:

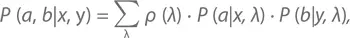
где ρ (λ) означает вероятность наступления ситуации λ.