Николя Жизан - Квантовая случайность. Нелокальность, телепортация и другие квантовые чудеса

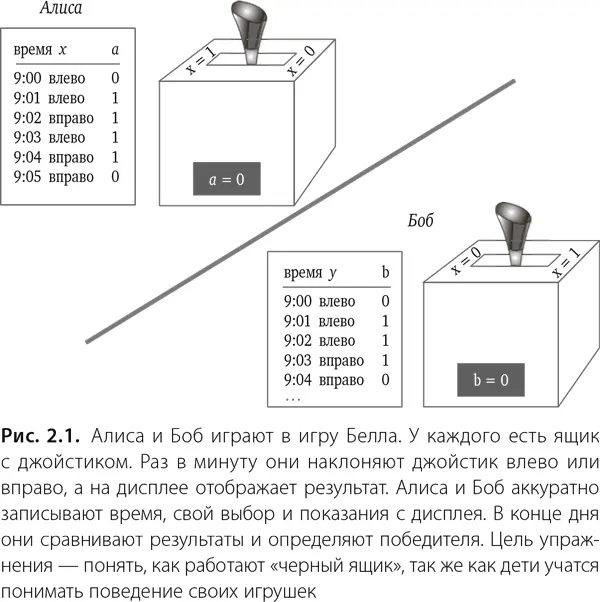
Перед началом игры Алиса и Боб берут по ящику, сверяют часы и затем удаляются друг от друга на некоторое расстояние. Ровно в девять утра и затем в каждую следующую минуту участники наклоняют свои джойстики в ту или иную сторону и аккуратно записывают показания, которые отображаются на дисплее, – время и результат собственного выбора. Важно, чтобы выбор правого или левого направления в каждую минуту был абсолютно свободным и независимым для каждого из участников. В частности, им не разрешено придерживаться одного и того же выбора, равно как и предварительно договариваться между собой. Важно также, чтобы ни один участник не знал о том, какое направление выбирает другой. Заметьте, наши друзья не жульничают, ведь они и вправду хотят понять, как работают приборы для игры Белла.

Они играют ровно до семи часов вечера, получив к концу дня 600 точек данных (примерно по 150 для каждого из случаев: лево-лево, лево-право, право-лево и право-право). Вечером они встречаются, чтобы подсчитать очки и получить общий итог игры.

Правила подсчета таковы:

1. Каждый раз, когда Алиса наклоняет джойстик влево, или Боб наклоняет джойстик влево, или оба они наклоняет джойстик влево, и при этом показания на дисплеях совпадают , участники получают одно очко.

2. Каждый раз, когда Алиса и Боб наклоняют джойстик вправо, и при этом показания на дисплеях различаются , участники получают одно очко.

Общий итог игры рассчитывается так:

• сначала для каждой из четырех комбинаций выбора (лево-лево, лево-право, право-лево и право-право) вычисляется коэффициент удачных попыток. Для этого количество полученных очков делится на общее количество попыток и затем все четыре коэффициента складываются. Максимально возможный результат игры равен 4, так как есть четыре варианта выбора и по каждому показатель успеха не превышает 1. Результат S должен означать, что Алиса и Боб выиграли S раз из 4. Заметим, что результат является средним и может быть принимать любое значение от 0 и 4. К примеру, результат 3,41 означает, что Алиса и Боб в среднем выиграли 3,41 раза из 4 или 341 раз из 400;

• мы увидим, что очень просто устроить ящики так, чтобы участники получали общий результат, равный 3. Поэтому иногда, говоря, что они победили в игре Белла, мы будем иметь в виду, что они выигрывали чаще, чем 3 раза из 4.

Для лучшего понимания этой странной игры давайте вообразим, что Алиса и Боб не записывают фактические показания с дисплеев, а просто выдумывают их. Другими словами, они независимо друг от друга выдают случайный результат [10] Заметьте, что так же можно объяснить ситуацию, в которой один из двух игроков играет добросовестно, а второй совершенно не следует правилам. В этом случае отношение успешных попыток к неуспешным также составит ½ с общим счетом 2. . В этом случае все четыре показателя удачных попыток к неудачным будут равны 1/2. К примеру, если половину отведенного времени Алиса и Боб записывают один и тот же результат, а вторую половину – противоположный, вне зависимости от направления наклона джойстика, то результатом игры будет 4 × ½ = 2. Чтобы получить счет больше 2, ящики Алисы и Боба не могут быть полностью независимыми друг от друга – они должны быть как-то связаны, скоординированы друг с другом, чтобы выдавать коррелированные результаты.

Если пойти чуть дальше, можно рассмотреть другой пример, в котором оба ящика всегда выдают одинаковые значения показаний, равные 0, невзирая на положение джойстика. В этом случае выбор Алисы и Боба никак не влияет на результат. Несложно подсчитать, что для каждой из трех комбинаций: «лево-лево», «лево-право» и «право-лево» – коэффициент удачных попыток будет составлять 1, а для комбинации «право-право» – 0. В этом случае общий счет будет равен 3.

Перед тем как рассмотреть принцип работы приборов, добавим чуть-чуть абстракции. Это подведет нас к самой сути понятия нелокальности.

Ученые любят описывать изучаемые объекты при помощи чисел, так же как сделали мы с показаниями ящиков Белла. Это помогает сосредоточить внимание на главном и не путаться в длинных предложениях вроде «Алиса наклонила джойстик влево и получила результат 0». Математический аппарат также помогает выполнять сложение и умножение, и мы увидим, что можно уместить понятие нелокальности в очень простом уравнении.

Сначала займемся Алисой. Пусть переменная х обозначает ее выбор, а переменная a – результат. К примеру, х = 0 будет означать, что Алиса выбрала наклонить джойстик влево, а х = 1 будет означать, что она наклонила его направо. Точно так же обозначим переменные для Боба: y будет обозначать его выбор, а b – результат. При таких обозначениях следующая небольшая таблица описывает случаи, в которых, согласно правилам, Алиса и Боб получают очко.

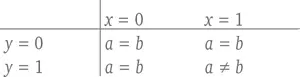
Оказывается, простые арифметические действия помогут нам свести всю игру Белла, в которой у Алисы и Боба имеется по ящику, которые далеко разнесены друг от друга, чтобы избежать какой-либо возможности копирования, где каждый из них делает свободный выбор и записывает результат, в одно элегантное уравнение:

то есть сумма а и b равна произведению х и у .

В самом деле, произведение х × у всегда равно 0, кроме случая, когда х = у = 1. Следовательно, говорит нам уравнение, сумма a + b всегда равна 0, кроме случая, когда х = у = 1.

Сначала рассмотрим случай, при котором x = y = 1. Сумма a + b при этом равна 1, а так как мы договорились, что переменные a и b могут принимать только значения 0 и 1, то уравнение a + b = 1 имеет два решения: или a = 0 и b = 1, или a = 1 и b = 0. Следовательно, если a + b =1, то a ≠ b . В этом случае в соответствии с правилами игры участники получают очко.

Теперь рассмотрим три оставшихся случая: ( x, y ) = (0, 0), (0,1) или (1,0). Во всех трех случаях произведение x × y равно 0, поэтому мы можем упростить уравнение до a + b = 0. Первое возможное решение – a = b = 0. Второе решение: это a = b = 1. Второе решение на первый взгляд кажется странным, потому что сумма 1 + 1 обычно равна 2. Но, так как мы считаем битами, нулями и единицами, результат также может быть представлен только как 0 или 1. В нашем случае 2 = 0 (математики сказали бы о сравнении по модулю 2). Следовательно, уравнение a + b = 0 эквивалентно a = b .