Константин Ефанов - Аппараты с перемешивающими устройствами

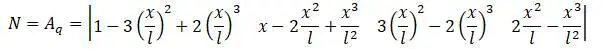
Делитация связана с перемещением:

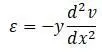
Для вектора деформации:

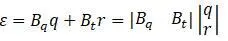
(составляющие деформации в зависимости от составляющих перемещений находятся применением матрицы оператора над матрицей интерполяционных функций).

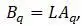
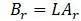
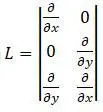
L – матрица-оператор, для плоских задач

A r – матрица интерполяции

Для матрицы интерполяции могут быть приняты функции вида:

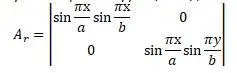
По уравнению :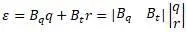

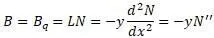
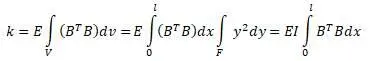
Пропуская математические выкладки, получается:

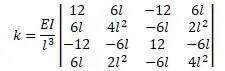
Для конечного элемента так как перемещения на концах равны нулю, матрица жесткости записывается в виде [20,с.505]:

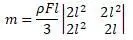
Теперь, подставив в уравнение 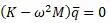матрицы получится:

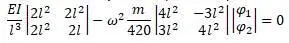
Вводится обозначение:

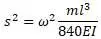
Характеристическое уравнение:

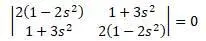
В виде многочлена (см. о решении уравнений в программе MathCAD):

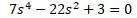
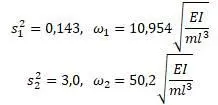
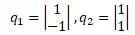
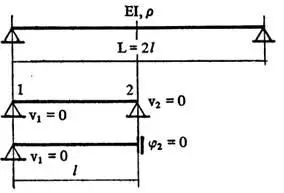
Для случая б), т.е. для второй части на рисунке выше, перемещение в узле 1 и вращение в узле 2 равны 0. С учетом этого матрицы k и m уменьшаются:

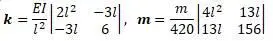
Характеристическое уравнение:

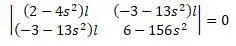
В виде многочлена:

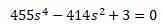
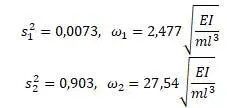
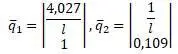
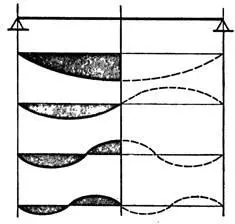
Эпюра собственных колебаний вала:

__

Итак, в разделе показаны теоретические основы расчета методом конечных элементов валов на свободные колебания.

Теорию можно сравнить с теорией ручного расчета по теории колебаний. Можно сделать вывод о том, что по теории колебаний применяется принцип Даламбера, для приближенного исследования колебаний используется метод Релея, а в расчетах по МКЭ используется вариационная формулировка по принцип Гамильтона с составлением и решением матриц.

Расчет по методу МКЭ является более обоснованным теоретически и позволяет выполнять расчет валов с мешалками и опорными узлами любой конфигурации.

Можно сделать вывод о том, что квалификации расчетчиков для расчетов ручным методом по теории колебаний и расчетов МКЭ являются приблизительно одинаковыми на основании сравнения сложности расчетных методик.

Нормативная методика по РТМ не выглядит обоснованной по сравнению с расчетами МКЭ и ручными расчетами по теории колебаний.

В настоящее время эффективность перемешивания определяется помещением индикатора в перемешиваемый объем аппарата (или лабораторной установки) и фиксацией времени и наличия установления равномерного распределения (окрашивания) индикатора по объему.

Такой подход нельзя считать полностью корректным. Определяются неоднородность перемешивания, распределение твердой фазы в жидком объеме др. параметры, определяющие качество перемешивания.

В вытяжной трубе при аэродинамических испытаниях автомобилей или авиационной техники, конструкцию обдувают окрашенной струей и фиксируют реакцию струи в части обтекания в зависимости от геометрической формы (конфигурации) конструкции.

Для мешалок необходимо объединить два указанных подхода.

То есть наметить структуру потоков в аппарате в зависимости от его геометрических параметров, затем выбрать мешалку, которая отбрасыванием потока жидкости от лопастей создает намеченную структуру потока. И по введению индикатора можно установить степень полноты распределения индикатора, как эффективность перемешивания.

__

Приведем структуры потоков для распространенных типов мешалок по данным Ф. Стренка [27,с.46]:

Также Ф. Стренк приводит направление тока для различных положений пропелерной мешалки [27,с.60]:

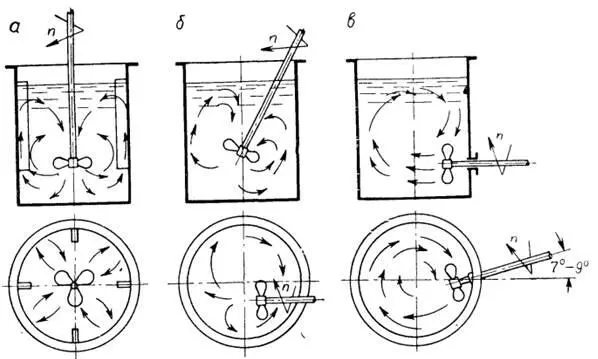
Стренк приводит изменение линий тока в зависимости от высоты установки мешалки в аппарате [27,с.104]:

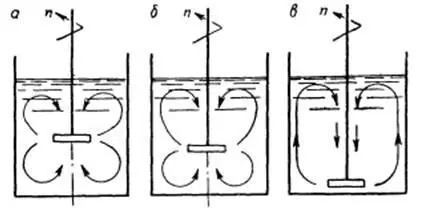
Для шнековой мешалки Ф. Стренк также приводит линии тока [27,с.65]: