Константин Ефанов - Аппараты с перемешивающими устройствами

Х , Х 1 – нормальные функции, решения которых отыскиваются для удовлетворения граничным условиям.

После подстановки:

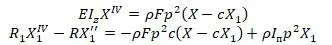
Тимошенко приводит пример стержня со свободно опертыми концами:

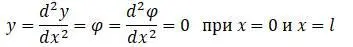
Функции Х и Х 1 в этом случае:

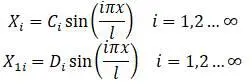
C i и D i – произвольные постоянные.

Вводятся обозначения:

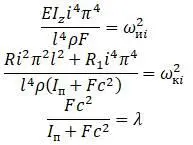
После подстановки получается:

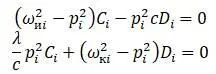
Решения для C i и D i находятся в случае, если определитель уравнений равен нулю.

В этом случае частотное уравнение:

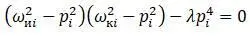
Из этой формулы:

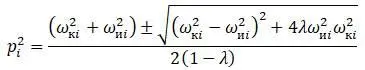
Для случая совпадения центра тяжести с центром сдвига, то есть с = 0 и λ =0 :

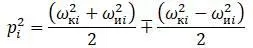
Из формулы получаются две системы значений частот:

Полученные частоты являются несвязанных друг с другом и независимых друг от друга частот изгибных (поперечных) и крутильных колебаний. Аналогичные результаты получаются для стержней с другими условиями закрепления концов.

Связанные изгибно-крутильные колебания можно найти методом Релея-Ритца [30,с.430].

__

Итак, по представленным данным Тимошенко возможен раздельный расчет на поперечные и крутильные колебания , либо расчет на изгибно-крутильные колебания методом Релея-Ритца.

Результат этого вывода может быть использован конструкторами для упрощения проблем проектирования валов с мешалками. То есть выполнять расчет поперечных колебаний и расчет крутильных колебаний по отдельности. Для определенных технических целей необходимо выполнение только одного из видов расчетов. Изложенная теория даст более глубокое понимание физики колебаний вала. Однако, правильно выполнять расчет на изгибно-крутильные колебания вала с мешалками.

Расчет изгибно-крутильных колебаний вала с мешалками по данным [32].

Рассмотрим шарнирно опертый стержень [32,с.200]. Система уравнений распадется на две независимые системы. Уравнение, описывающее только изгибные колебания в плоскости симметрии:

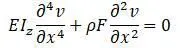
Уравнения, описывающие изгибно-крутильные колебания:

Граничные условия при x = 0 и x = l :

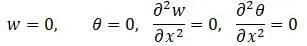
Граничные условия удовлетворяются при:

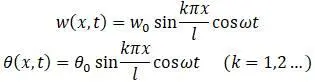
Собственные частоты определяются из формулы:

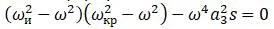
Частоты изгибных и крутильных колебаний :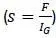

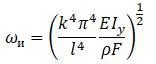
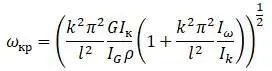
Собственные частоты колебаний:

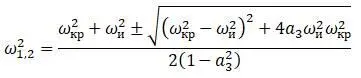
При a 3= 0 центр тяжести и центр изгиба совпадают,

__

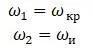
Как видно, формулы Тимошенко и по справочнику [32] для определения поперечных и изгибных колебаний почти полностью совпадают.

Однако, Тимошенко указывает о независимости от и необходимости применения метода Релея-Ритца.

__

Таким образом, для вала с мешалками как для балки по приведенной выше теории должны быть рассчитаны поперечные колебания, например, для неразрезной балки на трех опорах.

Затем должны быть рассчитаны крутильные колебания. Но в процессе перемешивания крутильных колебаний может и не возникать, в этом случае критические частоты будут строго соответсвовать поперечным частотам собственных колебаний. В случае наличия крутильных колебаний, их необходимо определить и проверку прочности выполнить для поперечных и крутильных колебаний.

Метод определения критической скорости по работе Тимошенко [31], где колебания связываются с эксцентриситетом необходимо считать некорректным. Колебания возникнут и при отсутсвиии эксцентриситета, однако, условия для статической балки и вращающегося вала с учетом эксцентриситета будут отличаться.

__

Тимошенко указывает о необходимости численного выполнения расчетов колебаний в работе [30]. То есть в том числе маститый специалист признает превосходство численных методов над ручными расчетами.

__

Итак, можно сделать следующий вывод: теорию колебаний можно применять для ручного расчета на практике, но она больше необходима для глубокого понимания физики процесса колебаний, а расчеты должны выполняться методом конечных элементов в специальном программном пакете, например, ANSYS.

В динамической задаче воздействие внешних сил является функцией времени. Напряженно-деформированное состояние зависит от времени. Время является дополнительным параметром, усложняющим расчет по сравнению со статическими расчетами.

Уравнения движения динамической системы выводятся с применением принципа Даламбера, на основе принципа возможных перемещений, на основе вариационного принципа Гамильтона.

Метода Даламбера удобно применять для систем с небольшим числом степеней свободы [20,с.486], к которым относятся валы с мешалками. Но вариационный подход Гамильтона является обобщением методов. Поэтому расчет вала с мешалками методом конечных элементов приведем на основе вариационного подхода Гамильтона.