Константин Ефанов - Аппараты с перемешивающими устройствами

Форма прогиба такая же как у статического прогиба под действием сил, применяя принцип Даламбера (приводя динамическое нагружение к статическому приложению сил).

Силы инерции вызывают дополнительный прогиб х 1 и х 2 . Их уравновешивают дополнительные силы упругости, возникшие из-за этого прогиба.

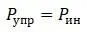
k 1 – прогиб в сечении I от силы равной 1 и приложенной в сечении I,

k 2 – прогиб в сечении I от силы равной 1 и приложенной в сечении II,

k 3 – прогиб в сечении II от силы равной 1 и приложенной в сечении I,

k 4 – прогиб в сечении II от силы равной 1 и приложенной в сечении II,

Сила инерции в сечении I:

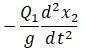
Сила инерции в сечении II:

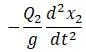
Сила равная 1 приложенная в сечении I вызывает прогиб k 1 , а сила инерции в этом же сечении вызывает прогиб:

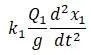
Прогиб в этом же сечении от силы инерции, приложенной в сечении II:

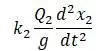
Полный прогиб в сечении I:

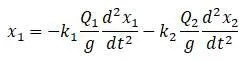
Полный прогиб в сечении II:

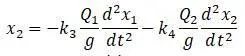
Полученные уравнения для х 1 и х 2 являются дифференциальными уравнениями движения для рассматриваемого случая трехопорного вала.

Коэффициенты в уравнениях находятся по принципу сложения сил, по которому прогиб в любой точке вала под действием сосредоточенных сил получается в виде суммы прогибов от каждой из силы по отдельности (для прогиба в сечении I находятся и суммируются прогибы от сил Q 1 , Q 2 , R C ).

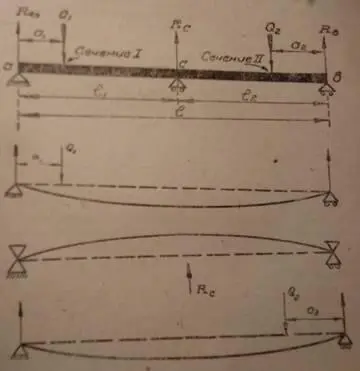
Уравнение упругой линии для левой части вала (с – расстояние между правой опорой и точкой приложением силы):

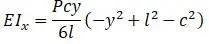
Прогиб в месте приложения груза:

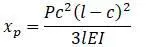
Находится неизвестная реакция опоры R C для статически неопределимого трехопорного вала (балки). Для нахождения реакции R C принципом сложения сил отбрасывается средняя опора вала и заменяется направленной снизу вверх реакцией R C . Так получается статически определимая система, нагруженная 3 силами: известными Q 1 и Q 2 и неизвестной реакцией R C . Сумма прогибов от каждой силы в точке с равна нулю так как в этой точке находится опора. И из условия равенства нулю прогибов находится реакция R C .

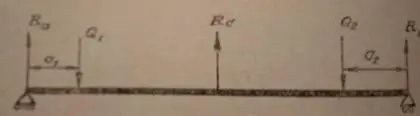
Прогиб от силы Q 1 в точке с :

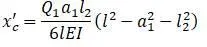
Прогиб от силы Q 2 в точке с :

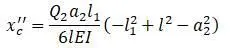
Прогиб от силы R C в точке с :

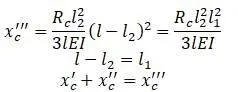
Вместо прогибов в формулу подставляются их значения:

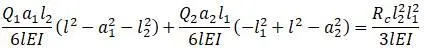
Из этоф формулы находится R c

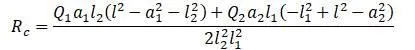
Находится прогиб в сечении I по известной R C . Прогиб равен сумме прогибов от сил Q 1 , Q 2 , R C

Прогиб в сечении I от силы Q 1 ( c = l – a 1)

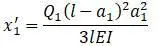
Прогиб в сечении I от силы R C ( c = l 2 и y = a 1)

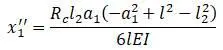
Подставляя значение R C

Прогиб в сечении I от силы Q 2 ( c = a 2 и y = l – a 2)

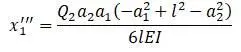
Суммарный прогиб в сечении

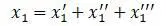
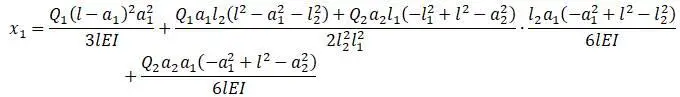
Формула прогиба в сечении I зависит от силы Q 1 и силы Q 2 . Группируются члены, содержащие силу Q 1 c получением формулы прогиба в сечении от силы равной Q 1 , приложенной в сечении I:

Если в эту формулу вести Q 1 = 1 , то формула покажет прогиб в сечении I от единичной силы, приложенной в сечении I:

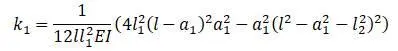
Если в полученном уравнении Q 2 = 1

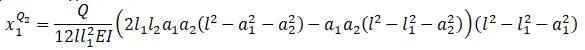
если в эту формулу вести Q 2 = 1 ,

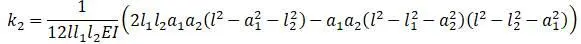
Прогиб в сечении II от силы Q 1

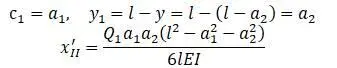
Прогиб в сечении II от силы R C

Прогиб в сечении II от силы Q 2

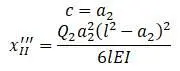
Полный прогиб в сечении II