Константин Ефанов - Аппараты с перемешивающими устройствами

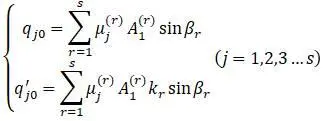
На основании приведенного выше, алгоритм полного исследования свободных колебаний системы с s степенями свободы состоит из следующих действий:

а) нахождение частот свободных колебаний k 1, k 2… k s из векового уравнения,

б) нахождение коэффициентов распределения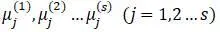

в) нахождения амплитуд 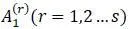и начальных фаз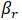

Применение программы MathCAD

Яблонский отмечает [3,с.143] если число степеней свободы превышает 4, то доя полного решения задачи потребуется громадная вычислительная работы.

Однако, в настоящее время возможно применение математических пакетов таких как MathCAD.

Программа MathCAD позволяет для матриц выполнять нахождение определителя, решать матричные уравнения. Применение этой программы исключает выполнение громоздких ручных расчетов и позволяет по приведенному выше алгоритму получать точное решение без каких-либо приближенных методов.

MathCAD позволяет выполнять с матрицами символьные вычисления.

Для решения матричного уравнения типа:

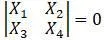
необходимо записать матрицу

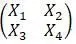
вставить определитель

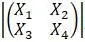
, вызвать команду «→».

В результате получается запись многочлена из определителя. Многочлен копируется в отдельное место. Выделяют переменную «Х» в многочлене и в панели инструментов выбирают полиноминальный коэффициент. В результате этого получится матрица с коэффициентами из полученного многочлена:

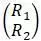
Затем вызывается или записывается вручную команда polyroots, в которую добавляется полученная матрица в виде:

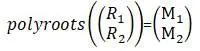
М 1 и М 2 –являются корнями матричного уравнения.

Для подробного ознакомления с вычислением матриц в MathCAD следует обратиться к учебному пособию по программе.

__

Рассмотрим пример построения эпюры свободных колебаний

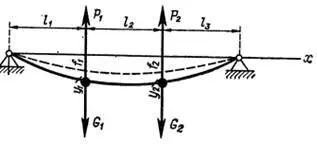
Находим значение кинетической и потенциальной энергии:

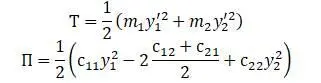
Находим коэффициенты инерции и жесткости системы:

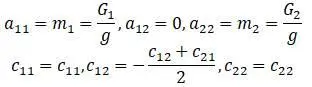
Для системы с 2 степенями свободы, уравнения частот записываются в виде:

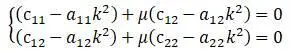
После выполнения операции исключения μ из системы двух уравнений, получается одно уравнение частот:

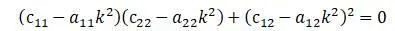
Корни уравнения частот

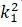
и

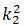
определяют частоты свободных колебаний

k

1

и

k

2

(частоты главных колебаний системы).

Частота k 1 ( k 1< k 2 ) является основной частотой колебаний.

Значения коэффициентов инерции и жесткости подставляются в полученное уравнение частот:

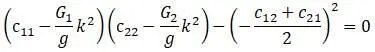
После преобразований:

В условии примера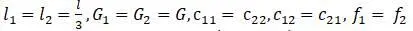

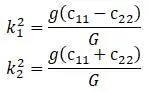
Корни:

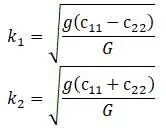
Значения частот k 1и k 2по результатам сопроматского расчета (см. работу Беляева [5]):

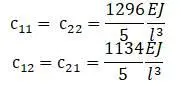
С учетом этого значения корней:

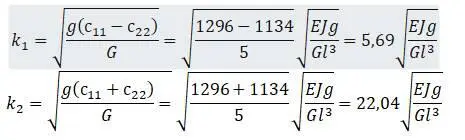
Коэффициенты распределения:

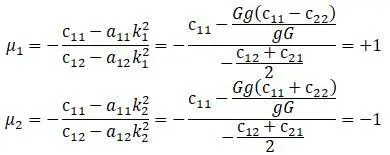
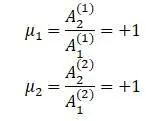
Эпюра главных колебаний:

__

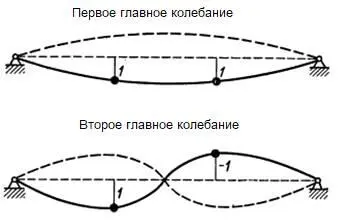
Форма эпюр подчиняется теореме об узлах собственных форм колебаний [4,с.120]. По этой теореме амплитуды для разных частот колебаний не имеют одинакового знака. То есть, если амплитуда первой формы положительная, то амплитуда остальных форм должна иметь минимально одну перемену знака. Число перемен знака или число узлов собственной формы колебаний m-го порядка равно m-1.

Бабаков [4,с.124] для балки с 3 точечными нагрузками приводит три возможные формы колебаний:

__

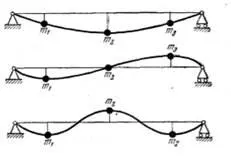
Решение приближенным методом Релея

По методу Релея допускается:

– масса системы не изменяет типа колебаний

– перемещение системы при колебании имеют ту же форму, что и при статической деформации (сходство формы не означает равенство величин деформации).

Ошибка по методу Релея не превышает 1,5% [2,с.60].

Метод Релея состоит в том, что в конкретный момент времени находится перемещение точек вала по формулам статической деформации. Для других моментов времени перемещения могут отличаться от выбранного момента времени. Так как действующая на вал сила Р , состоящая из веса груза и сил инерции 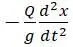зависит от времени.