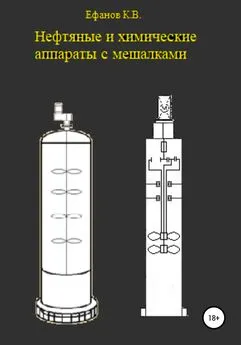
Константин Ефанов - Аппараты с перемешивающими устройствами
- Название:Аппараты с перемешивающими устройствами
- Автор:
- Жанр:
- Издательство:Array SelfPub.ru
- Год:2021
- ISBN:978-5-532-03611-6
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Константин Ефанов - Аппараты с перемешивающими устройствами краткое содержание
Аппараты с перемешивающими устройствами - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
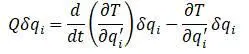
Силы, действующие на вал, зависят только от положения и не зависят от времени, скорости. В этом случае, согласно теоремы Кастильяно, обобщенная сила равна производной потенциальной энергии (при этом совершаемая работа переводит потенциальную энергию в кинетическую):
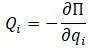
По теореме Кастильяно [5,с.319] прогиб точки приложения сосредоточенной силы ( P ) равен частной производной потенциальной энергии деформации по этой силе, а производная потенциальной энергии деформации по обобщенной силе равна обобщенному перемещению:
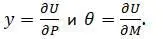
В результате получается уравнение движения Лагранжа :
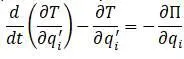
__
Равновесное положение системы вала принимается за начало обобщенных координат, т.е.
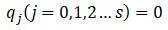
Кинетическая и потенциальная энергии системы:
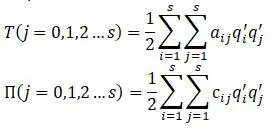
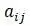
-
коэффициенты инерции,
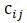
– коэффициенты жесткости.
Существует форма записи обобщенного закона Гука [5,с.314], связывающая все силы и перемещения:
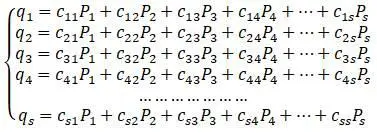
В условиях равновесия:
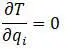
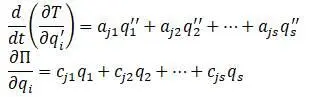
С учетом этого, уравнение Лагранжа можно записать в виде системы линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
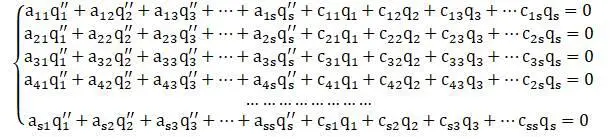
Частными решениями уравнений системы будут уравнения:
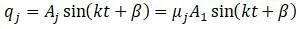
В частных решениях ( j = 0, 1,2,3…s ): 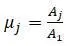
Частным решениям соответсвуют резонансные частоты колебаний.
Для неизвестных 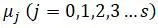 получают систему линейных однородных уравнений подстановкой полученного частного решения в приведенную систему уравнений (основные уравнения система малых колебаний с s степенями свободы):
получают систему линейных однородных уравнений подстановкой полученного частного решения в приведенную систему уравнений (основные уравнения система малых колебаний с s степенями свободы):
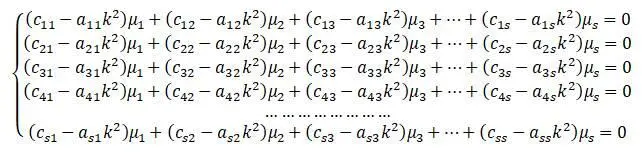
Полученная система уравнений имеет решение, отличное от нуля в случае равенства нулю определителя этой системы.
На этом основании записывается вековое уравнение (уравнение частот). Вековое уравнение является уравнением s -степени относительно :
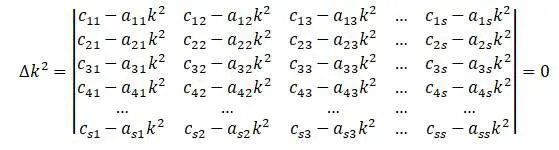
Искомые частота колебаний р и амплитуды μ , возникающие при этой частоте ( k = 1,2,3… n ), находятся из:
– основных уравнений системымалых колебаний с s степенями свободы,
– векового уравнения.
Вековое уравнение является уравнением s степени относительно k 2 . И из этого уравнения находятся все частоты свободных колебаний k системы.
Так как определитель Δ k 2= 0 , одно из уравнений системы при μ = 1 является следствием других уравнений системы. Последовательно подставляя в уравнения системы все полученные значения k 2 получается система уравнений:
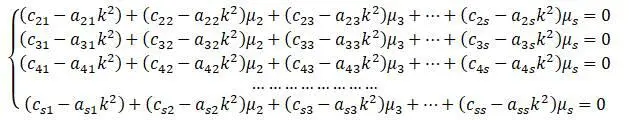
Находятся значения коэффициентов μ :
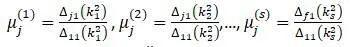
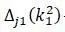
– определитель матрицы, получаемый вычеркиванием из определителя
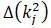
первых столбца и строки.
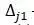
– минор элемента первой строки и
j
–го столбца со знаком (-1) основного
определителя 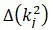
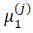
– коэффициенты распределения равные 1.
В результате частные решения первой системы уравнений:
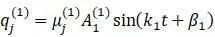
– первое главное колебание с частотой
k
1
и начальной фазой β
1
.
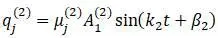
– второе главное колебание с частотой
k
2
>
k
1
и начальной фазой β
2
.
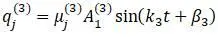
– третье главное колебание с частотой
k
3
>
k
2
и начальной фазой β
3
.
…..
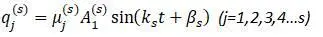
Коэффициенты 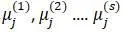 определяют форму главных колебаний:
определяют форму главных колебаний:
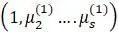
– форму первого главного колебания,
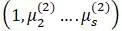
– форму второго главного колебания,
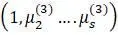
– форму третьего главного колебания,
и тд.
Общее решение первой системы уравнений можно получить суммированием частных решений:
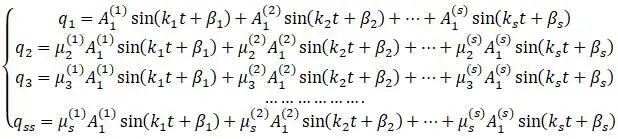
2 s неизвестные постоянных 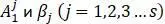 определяются по 2 s и по начальным обобщенным скоростям
определяются по 2 s и по начальным обобщенным скоростям 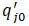 и координатам
и координатам 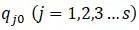 :
:
Интервал:
Закладка: