Константин Ефанов - Аппараты с перемешивающими устройствами

__

Рассмотрим по методу Релея колебания консольной балки (вала) с защемленным концом [2,с.73].

р – круговая частота собственных колебаний в этом примере и ниже.

Обобщенное перемещение :

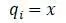
Кинетическая энергия груза:

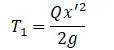
в этом уравнении квадрат скорости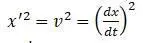

Кинетическая энергия элемента балки dc:

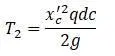
Уравнение упругой линии:

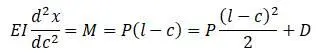
Минуя выкладки, полная кинетическая энергия системы:

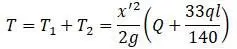
Потенциальная энергия системы:

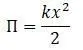
Уравнение Лагранжа:

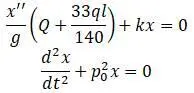
В этом уравнении круговая р 0 частота:

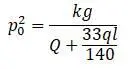
Статический прогиб на консоли балки:

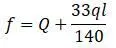
И

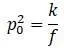
Решение уравнения :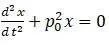

– период колебания

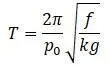
– частота

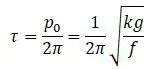
– круговая частота

__

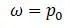
Рассмотрим по методу Релея колебания двухопорной однопролетной балки (вала), нагруженной сосредоточенной силой посередине [2,с.65].

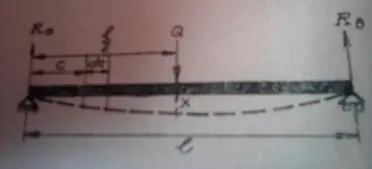
Обобщенное перемещение :

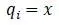
Кинетическая энергия груза:

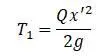
Уравнение упругой линии:

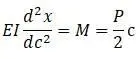
Интегрируя последовательно:

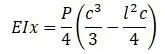
Прогиб:

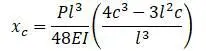
Прогиб посередине пролета:

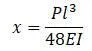
Следовательно,

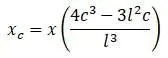
Как видно, прогибы x и x c являются динамическими прогибами, а не статическими, и имеют переменное значение, зависящее от времени.

Так, формула прогиба 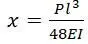имеет переменное от времени значение так как сила Р , состоящая из веса груза и сил инерции 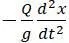зависит от времени.

Кинетическая энергия стержня:

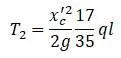
Полная кинетическая энергия системы:

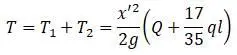
Потенциальная энергия системы:

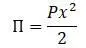
Уравнение Лагранжа:

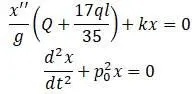
Эта формула аналогична формуле 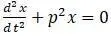движения груза, подвешенного на пружине, имеющий общий интеграл .

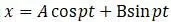Используя этот интеграл находим:

– период:

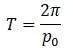
– частоту

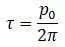
– круговая частота

Если собственную массу балки не учитывать:

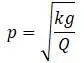
Т.е. к массе мешалки необходимо прибавить 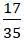от веса вала.

__

Рассмотрим по методу Релея колебания двухопорной однопролетной балки (вала), нагруженной сосредоточенной силой в произвольном положении [2,с.70].

Обобщенное перемещение :

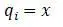
Кинетическая энергия груза:

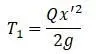
Кинетическая энергия элемента балки dc:

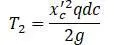
Уравнение изогнутой оси балки (вала):

В точке приложения груза:

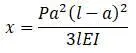
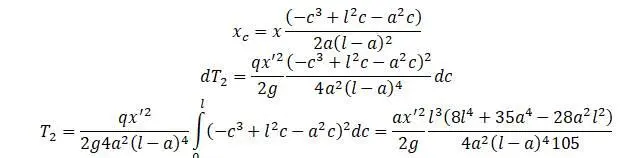
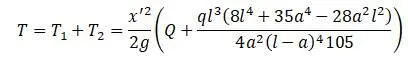
При 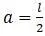формула имеет вид, как для предыдущего примера:

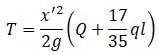
Потенциальная энергия системы: