Константин Ефанов - Аппараты с перемешивающими устройствами

Положительным расчетом вала на колебания является результат, по которому частота собственных колебаний не совпадает и не имеет близкого значения с критической частотой, т.е. с частотой вынуждающей силы.

При расчета по теории колебаний рассчитываются собственные и критические частоты. В случае их совпадения изменяется жесткость вала или устанавливается другая частота вынужденных колебаний.

Изменение жесткости вала связано с изменением статической деформации, которая связана со свободной частотой по формуле:

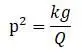
На резонансной частоте амплитуда вынужденных колебаний неограниченно возрастает при отсутствии внешних сопротивлений:

При наличии ограничителей колебаний, при резонансе амплитуды не превышают какого-либо максимального значения. Для валов мешалок в условиях отсутствия элементов, ограничивающих колебания, важно обеспечить расчетом отсутствие совпадения частот свободных колебаний и резонанса. При разгоне вала до рабочих оборотов, происходит быстрый переход через резонансную частоту, не оказывающий влияния на вал.

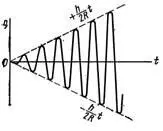
Для значений частот, близких к резонансной возникают биения вала. Для случая вала мешалки при отсутствии сопротивлений биению, колебания имеют вид:

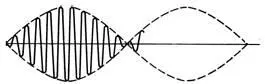
Затухающие биения при отходе от частот, близких к резонансным имеет вид:

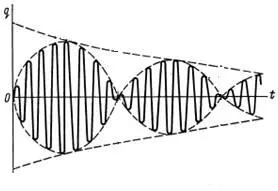
Для получения формулы вынужденных колебаний с учетом сопротивлений к внешним силам добавляют периодическую возмущающую силу 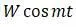(к внешним силам прибавляется сила 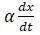препятствующая движению).

Упругие колебания системы с одной степенью свободы в общем случае (вторые два члена формулы относятся к вынужденным колебаниям):

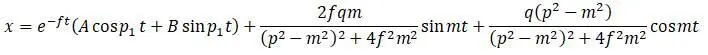
Уравнения для всех трех приведенных случаев колебаний можно получить из него как частные случаи:

– собственные колебания без учета сопротивлений ( f = 0, q = 0)

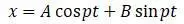
– собственные затухающие колебания (вынуждающая сила W = 0, )

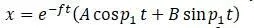
– вынужденные колебания без учета сопротивлений (, , в формуле получается, что первый член является вынужденными колебаниями, остальные два члена свободными колебаниями)

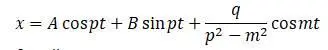
Формула вынужденных колебаний получается из вторых двух членов уравнения упругих колебания после отбрасывания свободных колебаний и замены в формуле

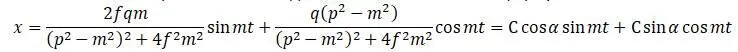
Т.е. вынужденные колебания являются гармоническими (так же как и собственные)

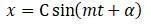
Амплитуда вынужденных колебания находится возведением в квадрат указанных двух членов формулы и последующим сложением:

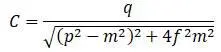
Как видно из формулы амплитуда вынужденных колебаний пропорциональна возмущающей силе, зависит от сравнительной частоты свободных р и вынужденных m колебаний, определяющих затухание свободных колебаний f .

При m < p амплитуда С приближается к статической деформации вала.

При m = p амплитуда С достигает больших величин, наступает явление резонанса вала .

В отсутствии сопротивлений произойдет разрушение вала через определенный промежуток времени.

При m > p амплитуда С стремиться к нулевому значению, колебания отсутствуют.

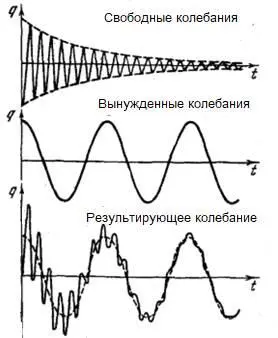
Приведем график амплитуд колебаний:

Как видно из рисунка, при резонансной частоте происходит разрыв кривой прогиба вала и разрушение вала.

При расчете вала необходимо не допускать наличия расчетных частот в пределах биения, то есть в пределах близких к резонансной частоте для недопущения разрушения вала. Запас может превышать критическую частоту на 20%. Такой запас, например, установлен для валов центробежных нефтяных насосов в ГОСТ 32601.

При сложении свободных и вынужденных колебаний получается результирующее колебание как результат наложения колебаний, колебание получается в форме биений:

Для описания положения мешалки используется обобщенная координата, то есть независимая величина, которая определяет изменение формы оси вала (положение системы).

Обобщенной силой является сила, которая полностью определяет действующую систему сил.

Обобщенная координата и сила связаны формулировкой: в результате произведения приращения обобщенной координаты на обобщенную силу получается работа.

Движение вала с мешалкой описывается уравнениями в обобщенных координатах. Между обобщенными координатами и декартовыми координатами всегда существует зависимость в виде функции декартовых координат от обобщенных координат.

Из общего уравнения движения системы, полученного в декартовых координатах, получают уравнение движения в обобщенных координатах. В результате получается запись:

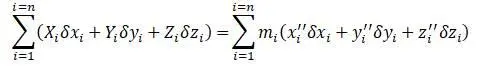
Для кинетическая энергия системы

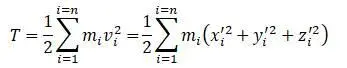
находится производная по обобщенным координате и скорости и после преобразований:

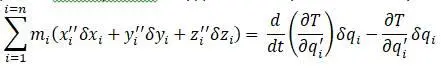
Уравнение движения запишется в виде