Константин Ефанов - Аппараты с перемешивающими устройствами

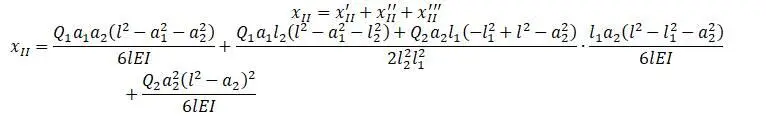
Группируя члены для сил Q 1 и Q 2 и принимая эти силы равными 1:

Теперь решаются уравнения прогибов х 1 и х 2 . Коэффициент k 3 заменяется на равный k 2 .

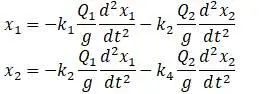
Вал совершает гармонические колебания:

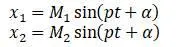
Производные этих последних уравнений по времени:

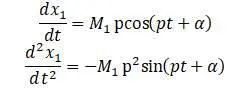
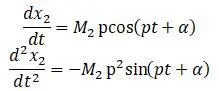
Теперь в полученные ранее формулы для х 1 и х 2 подставляются вторые производные:

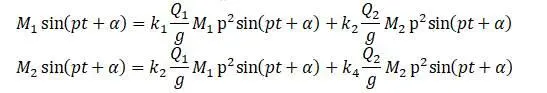
После преобразований:

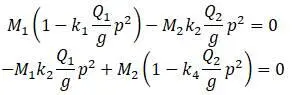
Для определения частоты р необходимо приравнять нулю определитель:

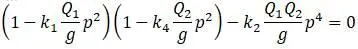
После группировки членов, содержащих р 2и р 4:

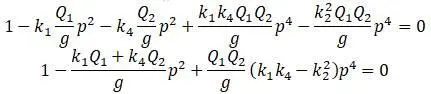
Полученная формула решается для нахождения р 2:

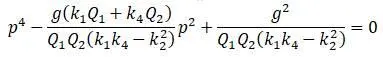
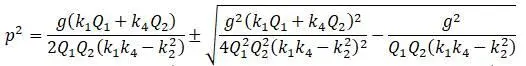
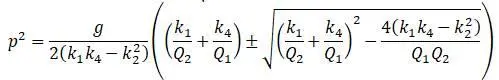
В результате решения получаются два значения частот, соответствующих двум возможным формам колебания вала. При первой форме два груза движутся вверх, при второй форме один груз движется вверх, а другой груз движется вниз.

Критические скорости вала:

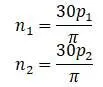
Аналогично двухпроленому валу находят частоты колебаний для многопролетных неразрезных валов.

__

Критические скорости валов относительно поперечных колебаний

Рассмотрим однопролетный вал с силой, приложенной посередине [2,с.97].

Вал жесткий:

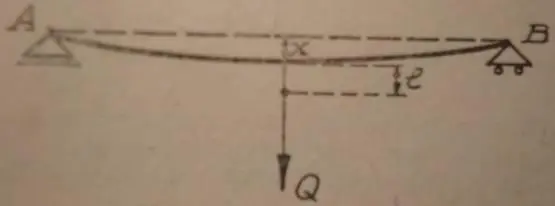
Массой вала пренебрегаем, центр тяжести нагрузки и ось вала не совпадают за счет неточности изготовления и прогиба системы от собственного веса.

При вращении возникает центробежная сила:

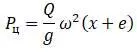
Внутренняя сила упругости:

Уравнение прогиба по условию равновесия:

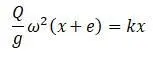
После решения относительно х :

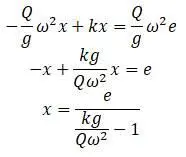
Вводится обозначение:

( р – круговая частота собственных колебаний)

Получается:

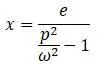
Из формулы видно, что при совпадении собственной частоты поперечных колебаний со скоростью вала прогиб стремиться к бесконечности и наступает явление резонанса.

Скорость вала, равная частоте собственных поперечных колебаний, является критической скоростью.

Критическое число оборотов вала:

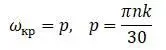
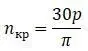
Нахождение критического числа оборотов вала состоит в задаче нахождения частоты собственных поперечных колебаний.

При скоростях свыше критической, центр тяжести вала устанавливается между точкой эксцентриситета на предыдущем рисунке и недеформированной осью вала.

Гибкий вал:

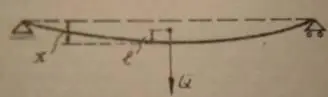
В этом случае формула 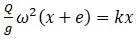изменится на формулу:

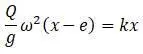
т.е. между х и e поменяется знак с «+» на «-».

Из этой формулы:

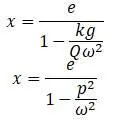
Из формулы видно, что с ростом скорости за пределом критической частоты прогиб вала стремится выпрямится. В пределе при x = e вал имеет прямую ось.

Лунц указывает [2,с.99] о доказательстве этого положения в работе Фепля и в работе Зоммерфельда.

__

Из формулы видно, что прогиб уменьшается с уменьшением 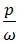или .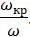

При конструировании вала необходимо уменьшать критическую частоту вала или равную ей частоту собственных поперечных колебаний вала.

Из формулы собственной круговой частоты

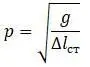
видно, что для уменьшения частоты р (равной критической) следует увеличить статическую деформацию вала. То есть сделать вал гибким, число оборотов которого выше резонансной частоты.

Здесь под гибким валом не понимается вал со свободно перемещающимся сечением и осью с двоякой кривизной [2,с.100].

Для изменения жесткости вала изменяют его длину, размеры сечения (инерциальные характеристики).

__

Приведем несколько отличающееся описание выкладок расчета критических оборотов вала в работе Тимошенко [31].

Тимошенко указывает [31,с.256] о возникновении критических колебаний вследствие эксцентриситета масс, возникших при изготовлении вала (биение поверхности).