Константин Ефанов - Аппараты с перемешивающими устройствами

Принцип Гамильтона записывается в форме [20]:

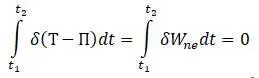
( Т и П – кинетическая и потенциальная энергии, W ne – силы демпфирования).

Функционал Лагранжа [20]:

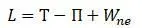
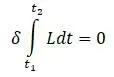
Функционал Лагранжа по принципу Гамильтона при возможных перемещениях удовлетворяет условиям совместности и граничным условиям на контуре в течении времени от t 1 до t 2 и имеет стационарное значение.

Начальное положение для вариационной формулировки МКЭ следует при Т = 0 и W ne = 0 :

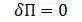
Введем зависимости для Т, П и W ne от обобщенных перемещений, скоростей и сил [20]:

После подстановки в интеграл и преобразований получим уравнение движения Лагранжа:

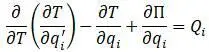
Для конечного элемента объема V [20]

– кинетическая энергия в матричной форме:

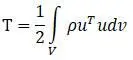
– потенциальная энергия (складывающаяся из внутренней энергии деформации, потенциальной энергии внешних объемных и внешних поверхностных сил):

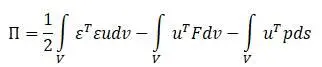
В конечном элементе поле перемещений и деформаций записываются интерполяционными функциями:

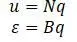
Скорость связана с обобщенной скоростью:

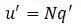
Силы демпфирования пропорциональны скоростям (являются неконсервативными):

Обобщенные силы в узлах конечного элемента при допущении о равномерном распределении сил демпфирования в единице объема, записываются формулой:

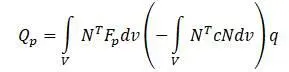
Формулы для кинетической и потенциальной энергии можно записать после преобразований в виде:

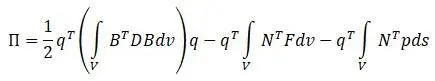
После подстановки записанных формул в первую формулу вариационной формулировки, получается матричная формулировка конечного элемента [20]:

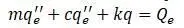
m – матрица масс, c – матрица демпфирования элемента, k – матрица жесткости, Q e – вектор обобщенных сил в узлах конечного элемента.

В результате составляется уравнение движения системы конечных элементов на основе уравнений движения одного (каждого) конечного элемента [20]:

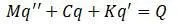
М – матрица масс, С – матрица демпфирования, K – матрица жесткости, Q – вектор обобщённых сил.

__

Собственные колебания вала находят решением последней записанной системы дифференциальных уравнений. Для колебаний без затухания, система запишется в виде [20,с.500]:

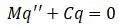
Матричное уравнение запишется в виде т.к. :

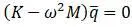
Уравнение имеет решение при равном нулю детерминанте системы: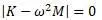

Матрица массы конечного элемента записывается формулой:

Для плоского линейного элемента перемещения описываются полиномами Гермита [20,с.491], матрица жесткости запишется:

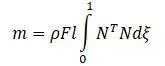
После преобразований [20]:

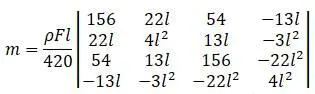
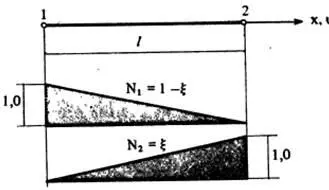
Для конечного элемента, показанного на рисунке выше, с нагрузкой вдоль оси и с узлами на концах, с применением линейных интерполяционных функций, матрица масс записывается в виде [20,с.492]:

Запишем формулу для матрицы жесткости.

На рисунке показан стержневой элемент под действием изгиба [20,с.69]:

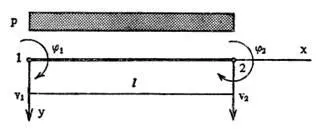
Вектор параметров перемещений в узлах элемента имеет два перемещения и два вращения:

Перемещение выражается в виде полинома с четырьмя суммированными координатами. Можно записать:

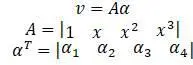
Угол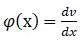

Перемещения и вращения на концах стержня:

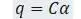
Матрица С [20,с.70]:

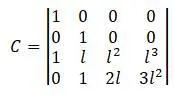
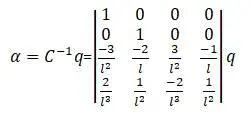
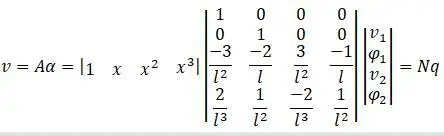
Матрица интерполяционных функций, посредством которой вводится связь между перемещениями на краях и для любой точки по оси стержневого элемента: