Анатолий Овчинников - Рассуждения об основах физики

Рис. 1. 3

Одновременность событий поясняется на рис. 1. 3. Здесь в координатах XOt изображена зависимость от координаты слагаемого переноса x/V e . Это прямая OC , наклонённая к оси OX под некоторым углом α, для которого tgα = 1 /V e . Назовем прямую OC прямой синхронизации. Прямая AB , параллельная прямой синхронизации замечательна тем, что события расположенные на ней одновременны, так как для точек этой прямой истинное время одинаково (например, t A = t B ). Пусть теперь часы двигаются вместе с подвижной системой X IO It I вдоль оси OX . При этом прямая синхронизации (теперь уже O IC I ) будет сдвигаться параллельно прямой OC , а значит и параллельно прямой AB , а потому t I A = t I B . Из этого следует, что если в одной системе координат события A и B одновременны, то они будут одновременны и в другой системе координат.

Ввиду важности понятия одновременности остановимся на этом подробнее. Рассмотрим высказывание: пусть в момент времени t координаты точки равны x,y,z . В мире математики это высказывание есть не что иное, как определение неявной функции четырех переменных в виде F(x,y,z,t) = 0. Однако в мире физики это высказывание можно трактовать как угодно, если не сделать дополнительного соглашения (между физиками и математиками). Каково должно быть это соглашение? Оно должно быть таково, чтобы высказывания физика и математика относительно реального мира были тождественны . Это следующее соглашение: отметки на часах о времени события, а также отметки на координатных осях о положении точки должны делаться за время равное нулю (далее кратко, нуль – соглашение). Это соглашение необходимо и полезно, потому что теперь математический аппарат приобретает физический смысл. Это соглашение в неявной форме всегда присутствует в «правильных» формулах физики.

Однако сторонник теории относительности полагает, что отметки на осях координат можно делать за время равное нулю, а отметки на часах о времени события нельзя сделать за время равное нулю. Как он это узнал? Ведь материальная точка может находиться на очень большом удалении не только от часов, но и от осей координат. Эта непоследовательность (а точнее, отказ от нуль – соглашения) и привела к «релятивистскому» понятию одновременности, когда два одновременных события в одной системе координат становятся уже неодновременными в другой системе координат.

Конечно, на практике, как при измерении координат, так и при измерении времени, мы всегда используем конечные скорости распространения сигнала. Но наши формулы должны быть устроены так, чтобы они все равно приводили бы к выполнению нуль – соглашения. Если они к этому не приводят, значит – они неверны. Нам приходится об этом говорить, потому что об этом забывают.

Резюмируем сказанное. Наша точка зрения такова. Сторонники теории относительности нарушили нуль – соглашение и это привело к появлению многочисленных «парадоксов». Но это на самом деле не «парадоксы». Это настоящие противоречия, «парадоксами» мы их называем по традиции. Ни одно из этих противоречий не было и не могло быть удовлетворительно разрешено в рамках теории относительности. Многочисленные попытки разрешить эти противоречия – яркие примеры того, как нужно «правильно рассуждать неправильно». Это потому, что нельзя разрешить противоречие, выдвигаемое теорией, с помощью этой же самой теории.

Пусть в начальный момент t χ = t = 0 материальная точка двигается из начала координат вдоль оси OX со скоростью V . Вместе с ней с этой же скоростью двигаются и часы ( V e и V одного направления). Когда точка и часы будут находиться в точке с координатой x , часы покажут время t χ . Это время состоит из двух слагаемых: 1-ое – истинное время движения точки t = x/V ; 2-ое слагаемое – слагаемое переноса часов x/V e . Таким образом:

Решая это уравнение относительно V, находим:

Эта формула отличается от обычной (классической) формулы наличием в знаменателе члена x/V e и он появляется потому, что мы учитываем материальность часов. Для идеальных (нематериальных) часов этот член равен нулю. Заметим также, что соглашение о направлении скоростей V e и V делает член x/V e всегда положительным. Запишем (1. 3) с применением производных

Или

Таким образом, начиная с формул (1. 4) и (1. 5) нам следует отличать величины: 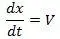– истинная (или исправленная) скорость точки, а 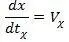– скорость этой же точки определяемая по показаниям часов традиционным методом, без учета материальности часов. Из (1. 5) видно также, что модуль скорости V всегда больше модуля скорости V χ.

Пусть относительно системы координат O 1X 1 со скоростью V 1 движется другая система O 2X 2, а относительно системы O 2X 2 со скоростью V 2 движется материальная точка и вместе с ней с той же скоростью двигаются и часы. Какова скорость точки V относительно системы координат O 1X 1 ? В начальный момент времени t χ= t = 0 положим координаты точки, часов и второй системы координат O 2X 2 равными нулю, относительно первой системы O 1X 1.

Время, отсчитанное часами по достижению точкой координаты x (в первой системе координат), равно 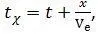а истинное время движения равно: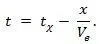

Путь, пройденный за это время системой O 2X 2 относительно системы O 1X 1 равен:

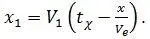
Путь, пройденный за это время точкой относительно системы O 2X 2 , равен:

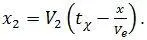
Путь, пройденный за это время точкой относительно системы O 1X 1 равен: