Анатолий Овчинников - Рассуждения об основах физики
- Название:Рассуждения об основах физики
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:2020
- ISBN:978-5-532-04232-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Анатолий Овчинников - Рассуждения об основах физики краткое содержание
Рассуждения об основах физики - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
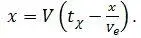
Этот путь равен сумме путей x 1 и x 2 , то есть:
x = x 1 + x 2 .
Из последних четырех равенств получаем:

Итак, для истинных времени и скоростей правило сложения скоростей классической механики остается в силе и никаких ограничений на величины скоростей при этом не накладывается.
С применением формулы (1. 6) нетрудно вывести аналогичную формулу и для векторов скоростей:

1. 9. Первый постулат
Как уже говорилось выше, для современной системы часов V e = c . Заменим в (1. 5) V e на c и получим:
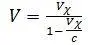
отсюда, выразив V χчерез V и c получим:

Пусть в выражении (1. 8) скорость V неограниченно возрастает. Тогда мы получим следующий предел:
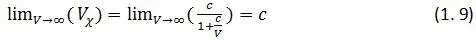
Выражение (1. 9) есть не что иное, как математическая запись 1-го постулата, именно : если скорость точки измерять по показаниям часов t χ , то измеренная таким способом скорость V χ, никогда не превысит скорости света . При этом истинная скорость точки V может превышать скорость света на сколько угодно. Итак, 1-й постулат появился только потому, что измеряя время реальными часами, мы полагаем, что они – идеальны. При учете материальности часов и введении формул перехода от показаний часов к истинному времени, 1-й постулат теряет силу и должен быть отменен.
1. 10. Преобразования координат
При справедливости формул сложения скоростей (1. 6) и (1. 7), нетрудно сделать вывод, что уравнения классической механики, в том числе законы сохранения импульса и энергии, остаются в классической форме, и во всех формулах должно фигурировать истинное время t . То же самое относится и к производным по времени, например:

Преобразования координат есть преобразования Галилея, с добавлением формулы перехода от показаний часов к истинному времени: 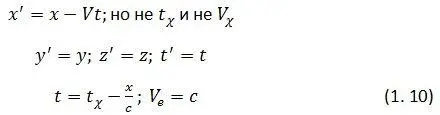
1. 11. Измерение массы ядер
В качестве примера того, как путаница между скоростями V χи V приводит к «странным» результатам, рассмотрим измерение масс ядер в масс-спектрометрах с применением магнитного поля. Измерение основано на приравнивании центростремительной силы силе Лоренца для частицы, движущейся в магнитном поле. Это уравнение таково:

Здесь: m – масса частицы, q – её заряд, r – радиус траектории частицы, B – индукция магнитного поля, V – скорость частицы.
Во времена Лоренца различие между V χи V не делалось, поэтому фактически уравнение (1.11) выглядит так:

Но теперь, когда мы знаем, что в центростремительную силу следует подставлять не V χ, а V равное
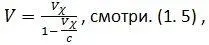
то исправленное уравнение для измерения массы будет уже другим:

Здесь m I – масса, измеренная с использованием уравнения (1. 13). Поделив (1. 12) на (1. 13) найдем отношение масс:

Поскольку с уменьшением массы частицы ее скорость V χв приборе возрастает, то из (1. 14) следует, что завышение массы, измеренное при помощи уравнения (1. 12) возрастает по отношению к массе, измеренной при помощи уравнения (1. 13) с уменьшением массы исследуемой частицы. Что нам следует ожидать, если при измерении масс ядер мы будем использовать уравнение (1. 13), а не (1. 12)? Нам следует ожидать, что, так называемый, «дефицит масс» станет равен нулю, а закон сохранения массы будет иметь силу и для микрочастиц.
1. 12. Второй постулат
Отмена 1-го постулата и переход к преобразованиям Галилея означает также и отмену 2-го постулата, потому что теперь скорость света ничем не отличается от остальных скоростей и подчиняется правилам классической механики, в частности правилам сложения скоростей (1. 6) и (1. 7). На этом можно было бы закрыть тему 2-го постулата, если бы не одно обстоятельство. Дело в том, что опровергнуть 2-й постулат можно и без того, чего изложено в данной главе. Коснемся этого вопроса по возможности кратко.
1. Второй постулат противоречит явлению Доплера. Пусть в точках A и B пространства расположены соответственно источник света и наблюдатель (или приемник). Рассмотрим движение волнового, светового цуга в пустоте от точки A к точке B [3, с. 33]. Его общая длина равна Nλ , где N – число периодов, а λ – длина волны. Согласно опытным фактам, этот волновой цуг всегда двигается по отношению к источнику со скоростью c . Если частота источника есть ν , то длина волны, скорость и частота связаны известным соотношением: c = λν . Заметим далее, что в пустоте фазовая и групповая скорости волнового цуга совпадают и равны c [3, с. 538]. Это означает, что волновой цуг, сколько бы он ни двигался, не меняет своей формы и длины волны λ . Это означает также, что длина волны зависит только от частоты источника ν и скорости света c (то есть λ = c/ν ) и не зависит ни от чего другого, в том числе и от наблюдателя.
Пусть сначала источник света и наблюдатель – неподвижны относительно друг друга. В этом случае наблюдатель измерит скорость, длину волны и частоту какие были заданы источником, то есть c,λ,ν . При этом волновой цуг двигается по отношению к наблюдателю со скоростью c .
Пусть теперь источник света и наблюдатель двигаются вдоль прямой AB относительно друг друга каким угодно образом и имеет место 2-й постулат. Но для наблюдателя этот случай ничем не отличается от предыдущего, так как и в этом случае, согласно 2-му постулату, скорость волнового цуга по отношению к нему продолжает оставаться равной c , а ν и λ , как мы уже говорили, не зависят от наблюдателя. Таким образом, наблюдатель измерит те же самые значения c,λ,ν , какие он измерил бы, находясь в покое относительно источника света. Для этого наблюдателя явления Доплера не существовало бы.
Читать дальшеИнтервал:
Закладка:










