Анатолий Овчинников - Рассуждения об основах физики

Кратко обсудим «релятивистскую» формулу эффекта Доплера:

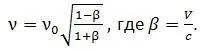
Если внимательно посмотреть на традиционные выводы этой формулы, то можно заметить, что в цепочке рассуждений и равенств имеют место высказывания, основанные как на классической механике, так и на «релятивистской» и в этой цепочке они чередуются. Поэтому, строго говоря, эту формулу следует называть «гибридной». Она не отражает реального положения дел. Так, например, для случая встречного движения источника и приемника (и положив β > 0) формула будет выглядеть так:

Таким образом, эта (гибридная) формула приводит к нарушению закона сохранения энергии. Настоящей «релятивистской» формулы эффекта Доплера не существует; она запрещена 2-м постулатом.

2. Второй постулат противоречит явлению интерференции и образованию стоячих световых волн. Хорошо известно, что «релятивистская» формула сложения скоростей есть следствие 2-го постулата и выглядит так [2, с. 371]:

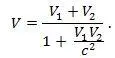
Из этой формулы следует, что относительная скорость двух световых волновых цугов всегда равна c , как при интерференции, так и при образовании стоячих световых волн. Если бы это было так, мы никогда не наблюдали бы, ни интерференции, ни стоячих световых волн. Потому, что не нашлось бы ни одного конечного промежутка времени, для которого разность фаз двух волновых цугов была бы постоянной. Природа предпочитает складывать скорости по классическим, а не по «релятивистским» правилам, поэтому относительная скорость двух волновых цугов, покидающих один и тот же источник (в одном направлении) равна нулю, а не c и это обстоятельство позволяет нам наблюдать явление интерференции.

3. Кратко о многочисленных опытах, которые будто бы подтверждают 2-й постулат. Анализ этих опытов показывает, что в них экспериментатор имеет дело не с движущимся источником света, а с неподвижными источниками света, каковыми являются детали самих приборов. К ним относятся: стеклянные пластинки, призмы, стеклянные объективы, полупрозрачные зеркала, дифракционные решетки. Все эти детали являются источниками собственных волновых фронтов, как правило, с сохранением частоты падающих на них волновых фронтов (это явление иногда называют «переизлучением»). Это не противоречит закону сохранения энергии. Итак, информация о скорости света и длине волны от движущегося источника света теряется в самом приборе. Поэтому такие опыты не подтверждают и не опровергают 2-й постулат . Уникальным с этой точки зрения является идеальное зеркало. Оно сохраняет при отражении, как длину волны, так и модуль скорости падающего на зеркало света. Однако зеркальные интерферометры в таких опытах не применялись. Можно предложить проект зеркального телескопа-интерферометра для астрономов. Но он, по-видимому, опоздал, потому что сейчас уже понятно, что наблюдения таким телескопом опровергнут 2-й постулат.

4. Наконец, добавим, что современная наука продолжает накапливать опытные факты отнюдь не в пользу 2-го постулата; см. [4].

Мы принципиально отказываемся рассматривать время, как составляющую четырехмерного пространства-времени. Такое рассмотрение неизбежно приводит к противоречиям с опытными фактами. Мы принципиально признаем время скалярной величиной.

Дадим определение времени, используя в качестве основных величин координаты и скорость материальной точки. Пусть r– радиус вектор материальной точки; v( x,y,z ) – вектор скорости этой точки, как функция координат; d r– дифференциал вектора r; V – модуль скорости. Назовем все указанные векторные величины нормированными по скорости, если они поделены на модуль скорости, то есть: r/ V ; d r/ V; v/ V , из которых последний вектор есть не что иное, как безразмерный единичный вектор того же направления, что и вектор v. Дифференциалом времени dt назовем скалярное произведение:

Временем физического процесса назовем криволинейный интеграл от (1. 15) взятый по траектории движения ( l ) материальной точки от точки (траектории) A до B :

Здесь и далее под выражением 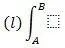следует понимать единый символ криволинейного интеграла по кривой ( l ), а не произведение ( l ) на интеграл.

При V = 0 выражения (1. 15) и (1. 16) становятся неопределенными. Физический смысл этого таков: в системе, где ничего не движется, понятие времени теряет смысл и не является необходимым для полного описания системы.

Как известно из векторной алгебры, скалярное произведение (у нас (1. 15) и (1. 16)) не зависит от замены координат. Поэтому у нас время t AB , дифференциал времени, а также одновременность событий являются инвариантами по отношению к преобразованию координат.

Назовем часами устройство перемножающее скалярно некоторый нормированный эталонный вектор скорости v e/ V eна нормированные векторы r/ V eи s e/ V e; где r– радиус вектор часов, а s e– некоторый эталонный вектор, встроенный в часы и всегда того же направления, что и вектор v e. Часы суммируют результаты умножения по правилу:

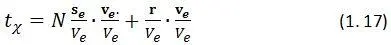
Здесь N – число периодов часов. Второе слагаемое в (1. 17) есть не что иное, как слагаемое переноса часов. Если часы при измерении времени находятся в покое в начале координат, то тогда:

Именно это время и является эталонным временем для сравнения с ним времени физического процесса. Измерить время t AB это значит узнать при каком k имеет место равенство:

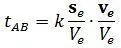
Это время равно интегралу (1. 16) то есть:

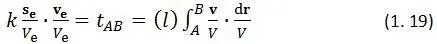
Если часы двигаются по кривой ( l ) от точки A до точки B независимо от других скоростей, то слагаемое переноса часов t пбудет равно интегралу: