Анатолий Овчинников - Рассуждения об основах физики

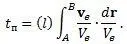
При этом скорость v eнаправляется по касательной к траектории движения часов в заранее выбранном положительном направлении. Другими словами: слагаемое переноса часов равно времени, которое затратит материальная точка, двигаясь по данной кривой вместо часов со скоростью равной v e. В другом случае при измерении времени часы могут двигаться вместе с материальной точкой, время движения которой они измеряют. Тогда на часах кроме времени (1. 19) появится еще слагаемое переноса часов, которое будет равно интегралу:

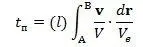
Здесь под знаком интеграла вместо множителя v e/ V eспециально поставлен единичный вектор v/ V , который подчеркивает, что согласно прежней договоренности, при таком движении мы направляем вектор v eпо направлению вектора v. Итак, показания часов будут равны сумме:

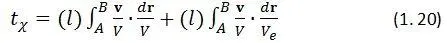
Здесь первое слагаемое – истинное время t , второе слагаемое – слагаемое переноса часов.

С точки зрения математика, введенное нами определение времени, допускает процессы, длительность которых равна нулю. Это такие процессы, в которых векторы d rи vперпендикулярны. Гипотеза о том, что и в природе существуют такие процессы, заслуживает отдельного изучения. Если эта гипотеза действительно имеет место, то нас уже не будет обескураживать тот факт, что сферический световой волновой фронт стягивается в материальную точку (квант) за время равное нулю. При таком преобразовании вектор скорости волнового фронта vперпендикулярен вектору d r. Точнее говоря: если волновой объект представляет собой шаровой слой, ограниченный двумя сферами (в пространстве) толщиной Δ s , то время его преобразования в точку (у нас в световой квант) будет равно: Δ t = Δ s / c , то есть будет равняться длительности волнового цуга (во времени).

1.Первый и второй постулаты теории относительности есть следствия попыток объяснить результаты физических измерений без учета того факта, что часы, будучи материальным объектом, обладают присущими таким объектам свойствами (слагаемым переноса).

2.Учет этого факта меняет взгляды на измерение времени и приводит к отмене этих постулатов.

3.Преобразования Лоренца отменяются и заменяются преобразованиями Галилея с добавлением формулы перехода от показаний часов к истинному времени.

4.Все рассуждения, в которых применялись преобразования Лоренца, следует пересмотреть заново.

5.Скорость света переходит в разряд обычных скоростей и подчиняется, как и все остальные скорости, правилам классической механики.

О возможности измерений в теории относительности (точнее об их невозможности) уже говорилось кратко в [1, с. 4 – 7]. В предыдущей главе мы также показали, что неправильное применение часов при измерении времени приводит к появлению двух ложных постулатов (с которых и начинается теория относительности). Однако, просмотр дискуссий, которые ведутся по вопросу измерений в теории относительности (например, на сайте РАН, forum. lebedev. ru) показал, что имеет место досадное непонимание этой проблемы. Становится ясно, что об этом надо писать более подробно (что и делается в этой главе).

Нетрудно видеть, что все измерения в физике в конечном итоге сводятся к измерению относительных перемещений (или длин), а также углов. Связь между измерениями в физике и законами геометрии является важнейшей особенностью законов природы. Поэтому нам достаточно разобраться с вопросом об измерении длины в теории относительности. Если возможность измерений длины в теории относительности будет доказана, то и все остальные измерения в этой теории также будут заслуживать доверия. И наоборот, если будет доказана невозможность измерений длины в этой теории, то и все остальные измерения также уже не будут иметь смысла. Как раз последнее мы и намерены сделать. Наша цель: доказать, что в теории относительности понятие измерения длины не имеет смысла, а также объяснить читателю, почему это происходит. Заметим, что возможность измерений в какой-либо теории не является фактом само собой разумеющимся. Существует много теорий, в которых нет понятия измерения (например, топология). В общем случае возможность измерений необходимо или подтверждать или опровергать. Для классической механики мы подтвердим возможность измерений попутно.

Заметим еще, что разговор об измерениях в теории относительности может завести нас очень далеко. Мы ограничимся лишь тремя замечаниями (см. пункты 2. 6 – 8). Эти замечания (вытекающие из обсуждения проблемы измерений), совершенно необходимо довести до сведения читателя, как весьма важные.

И начнем мы наше изложение с рассуждений о длине движущейся линейки.

Итак. Пусть в системе координат S ( x,y,z ) покоится линейка на оси OX и её длина равна L 0. Пусть вдоль оси OX двигается со скоростью V вторая система координат S I (оси OX и O IX I совпадают по направлению). «Измерение» длины линейки в системе S I можно производить двумя способами.

1-й способ (по Эйнштейну). Отметки начала и конца линейки на оси O IX I делаются одновременно в системе S I . И тогда мы получим длину линейки равной, [2, с. 373]:

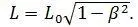
2-й способ (по антиЭйнштейну). АнтиЭйнштейн скажет: «Господа, какая же это длина линейки, если отметки делаются не одновременно по часам, установленным на её концах? Ведь за время между отметками линейка успеет сдвинуться по отношению к S I на некоторую величину Δ L . И это уже не будет длина линейки, а будет длина:

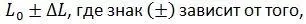
какая из отметок будет сделана первой. Поэтому отметки должны делаться одновременно относительно концов линейки» (т.е. одновременно в системе S ). И тогда, поступив таким образом, антиЭйнштейн получит длину линейки в системе S I равной [2, с. 376]:

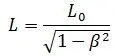
Какой из этих способов правильный? Эйнштейн и его последователи не предусмотрели ответа на этот вопрос (по крайней мере, вразумительного). По их мнению, 1-й способ «естественный». Но 2-й способ ничуть не менее «естественный». В обоих способах одновременность присутствует. Некоторые говорят, что здесь мы имеем два различных опыта. Но это не так. Физический опыт один и тот же (ни L 0ни V не зависят от количества наблюдателей и их мнений). Опыт один; действия же наблюдателей различны и приводят к различным результатам. И тут вступает в дело принцип относительности, который усложняет ситуацию и делает её неразрешимой. В самом деле. Если «измерения» идут по 1-му способу, то наблюдатель в системе S I скажет: «Кто говорит, что линейка в моей системе стала короче? Линейка в моей системе не изменилась. Это линейка в системе S стала длинней». Если «измерения» идут по 2-му способу, то наблюдатель в системе S I скажет: «Кто говорит, что линейка в моей системе стала длинней? Линейка в моей системе не изменилась. Это линейка в системе S стала короче». Итак, наблюдатель в системе S I говорит то же самое, что и наблюдатель в системе S , но он всегда говорит все «наоборот», потому, что действует принцип относительности. Ни законы природы, ни логики не дают нам возможности узнать какая из четырех перечисленных выше линеек правильная (истинная). Далее мы увидим, что изложенные выше способы «измерения», ни каким образом не подходят под понятие – измерение. Поэтому слово «измерение» в этом пункте всюду заключено в кавычки.