Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Если частица движется произвольно, то ее путь будет представлен кривой, а котангенс угла наклона касательной к оси x в какой-либо точке будет равен скорости частицы в момент, соответствующий этой точке.

Как в СТО, так и в общей теории относительности (мы увидим это позднее) ключевым понятием является метрическое пространство . Под этим понимается некое множество точек, переход между которыми осуществляется непрерывным образом и определено понятие расстояния между ними. Вспомним обычное пространство Евклида. Квадрат расстояния r между началом координат и точкой с декартовыми координатами x, y, z определяется по правилу: r 2= x 2+ y 2+ z 2.

Эта величина всегда положительная, за исключением случая, когда длина равна нулю.

Пространство Минковского тоже метрическое. Однако в нем расстояние между двумя точками называется интервалом и определяется непривычным образом. Квадрат интервала s между началом координат и какой-либо точкой 4-мерного пространства-времени (рис. 5.2) определяется по правилу:

s 2= c 2 t 2– x 2– y 2– z 2= c 2 t 2– r 2.

Временную координату ct и пространственные координаты Декарта x, y , и z , представляющие единую координатную сетку в пространстве Минковского, обычно называют координатами Лоренца . Как видно, временная и пространственные части в определении интервала входят с разными знаками. Из-за этого квадрат интервала может быть положительным, нулевым и даже отрицательным. Пространства, в которых расстояния определяются таким образом, называются псевдоевклидовыми .

Итак, пространство Минковского – это псевдоевклидово метрическое пространство, объединяющее время (длительность) и пространство (протяженность, 3-мерное пространство Евклида).

Точки в пространстве Минковского называют событиями или мировыми точками . Таким образом, каждой мировой точке соответствует момент времени и точка в 3-мерном пространстве. А интервал – это расстояние между двумя мировыми точками или, в ряде интересных случаев, промежуток времени между двумя событиями.

Теперь попытаемся понять, как в рамках исходной системы отсчета в пространстве Минковского выглядит другая инерциальная система отсчета. Оси 0 ct и 0 x (см. рис. 5.2) в исходной системе образуют базис. Путь наблюдателя, связанного с исходной системой, направлен вдоль оси 0 ct. Для него же ось 0 x и параллельные ей линии – это сечения одновременности. Наблюдатель другой инерциальной системы движется прямолинейно и равномерно по отношению к первой. Тогда ясно, что его путь направлен вдоль наклонной прямой, например, 0 А на рис. 5.2. Для движущегося наблюдателя сечения одновременности также наклонятся. Остается сделать вывод: чтобы перейти к базису движущейся инерциальной системы отсчета нужно осуществить поворот исходного базиса. При этом угол поворота соответствует относительной скорости между системами. Вспомним, что две системы отсчета связаны преобразованиями Лоренца. Именно поэтому такие повороты базиса называют лоренцевыми вращениями .

На рис. 5.3 на диаграмме пространства Минковского изображен базис неподвижной системы K с нештрихованными координатами, и базис движущейся в направлении оси 0 x со скоростью V инерциальной системы отсчета K’ с штрихованными координатами. Теперь выпишем преобразования Лоренца от одних координат к другим:

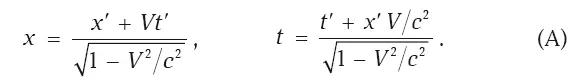
Преобразования дают возможность заключить, что обе системы отсчета эквивалентны. Действительно, если выразить штрихованные координаты через нештрихованные, то получим те же самые преобразования:

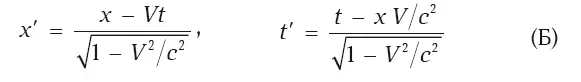
с заменой знака «плюс» перед V на «минус» – по отношению к штрихованной системе нештрихованная движется в противоположном направлении.

Одно из достоинств геометрической интерпретации пространства Минковского состоит в том, что лоренц-инвариантность выражается в инвариантности относительно лоренцевых вращений. В частности, значение интервала, записанного выше, не изменяется после поворота базиса, хотя теперь выражается через новые (штрихованные) координаты нового базиса. Чтобы убедиться в этом нужно лоренцевы преобразования (А) подставить в выражение для квадрата интервала, записанного выше. В результате получим

s 2= c 2 t′ 2– x′ 2– y′ 2– z′ 2= c 2 t′ 2– r′ 2.

то есть s = s’ .

В инвариантности интервала нет ничего удивительного – это лишь геометрическое свойство пространства Минковского, а не следствие каких-то принципов. Действительно, поскольку интервал – это длина в метрическом пространстве, то эта величина не зависит от способов измерения (использования той или иной координатной сетки). Замечательно другое – известные геометрические свойства псевдоевклидовых пространств оказались весьма полезными для описания СТО.

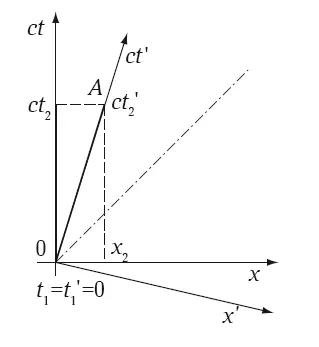
Рис. 5.3. Переход к другой инерциальной системе на диаграмме пространства Минковского

Эффекты сокращения длины, замедления времени, сложение скоростей в СТО являются следствием лоренц-инвариантности. Остановимся на первых двух. Рассмотрим линейку, собственная длина которой l 0– это длина в ее системе покоя. Пусть система покоя для выбранной линейка – это система K’ , которая движется относительно нас (системы K) со скоростью V . Тогда, если концы линейки имеют координаты

x 1 ′ и x 2 ′ , то l 0= x 2 ′ – x 1 ′ .

Определим длину этого отрезка с точки зрения наблюдателя системы K . Для этого нужно в один и тот же (!) момент времени t определить координаты концов линейки x 2и x 1в системе K . Тогда для нас длина линейки буде иметь величину l = x 2– x 1. Чтобы определить каждое из значений x 2и x 1через соответствующие штрихованные координаты используем первую часть преобразований Лоренца (Б) каждый раз с одним и тем же значением t. Затем составим разницу и получим 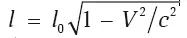, то есть для нас (покоящейся системы K ) движущаяся линейка становится короче.

Подтвердим вывод о замедлении времени. Находясь в системе K, будем отслеживать ход часов в системе K′ , которые находятся в точке x′. Для нас часы в системе K идут одинаково во всех точках, поэтому часы системы K′ можно сравнивать с любыми нашими. Не теряя общности, можно предположить, что x′ = 0 и моменты первого сравнения в обеих системах также нулевые: t 1 ′ = t 1= 0. Вопрос в том, как начнут разниться показания в любой следующий момент сравнения t 2(а для системы K′ – t 2 ′ ). Теперь удобнее использовать вторую часть преобразований Лоренца (А). Получаем 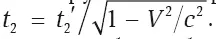. Как видно, показания часов в нашей системе K будут больше, чем в K′ , хотя в обоих случаях отсчет начинался с нуля. Таким образом, движущиеся часы идут медленнее.