Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Представления о пространстве Минковского помогают разобраться и с так называемым парадоксом близнецов . Он связан с эффектом относительного замедления времени. Это мысленный эксперимент, в котором рассматривают двух близнецов, один из которых решил отправиться в космическое путешествие. В соответствии с релятивистским замедлением времени каждый из близнецов считает (и это подтверждается его наблюдениями), что часы другого близнеца идут медленнее, чем его собственные. Но тогда, когда путешественник вернется, окажется, что каждый из них должен обнаружить своего брата моложе, чем он сам! Это и есть парадокс. Так кто из них будет моложе при встрече после путешествия?

На самом деле парадокс сформулирован точно так же, как многие детские загадки, когда важные детали замалчиваются. Об их существовании нужно догадаться.

Парадокс был бы, действительно, парадоксом, если бы положение близнецов было симметричным. Но так ли это? Путешественник, прежде чем полететь к звездам, должен разогнаться до высоких скоростей, потом, где-то там далеко, развернуться, а вернувшись к Земле, замедлиться, чтобы встретиться со своим братом. Ничего этого не происходит с братом-домоседом. Как минимум, во время трех периодов своего путешествия космонавт будет испытывать ускорения. Поэтому, строго говоря, на пространственно-временной диаграмме мировая линия брата-путешественника будет кривая.

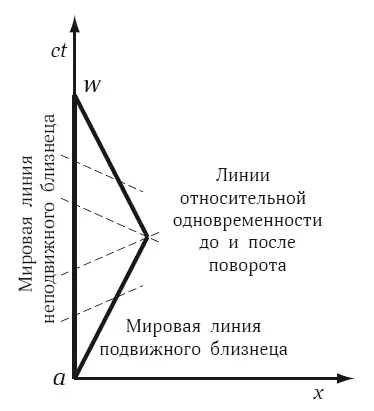
Рис. 5.5. Решение парадокса близнецов

Качественно проблему можно решить, представив мировую линию путешественника в виде ломаной, состоящей из двух отрезков, как показано на рис. 5.5, ускорения «скрыты» в изломах этой ломаной. Мировая линия брата-домоседа совпадает с осью времени. Сравним интервал отрезка прямой на оси времени между событиями a (расставания) и w (встречи) с суммой интервалов отрезков ломаной. Прежде всего, отметим, что наклонные отрезки ломаной линии времениподобные, поскольку описывают движение материального тела. Но тогда из наших рассуждений о сравнении интервалов на рис. 5.4 следует, что интервал каждого из наклонных отрезков меньше половины интервала отрезка aw , то есть интервал всей ломаной меньше, чем весь интервал aw. Но интервал отрезка мировой линии наблюдателя равен промежутку его собственного времени. Поэтому брат-путешественник при встрече будет моложе.

Тот же вывод можно сделать по-другому. Нанесем на наклонных мировых значения собственного времени путешественника и соединим их с точно такими же значениями для времени на мировой линии домоседа. Получим два набора параллельных линий, как на рис. 5.5, первый набор синхронизован на момент их разлуки и в будущее, второй набор синхронизован от момента встречи и в прошлое. Эти наборы параллельных линий всегда про-странственноподобны, они не имеют никакого отношения ни к световым конусам, ни к реальным наблюдателям. Очевидно, домосед проживет больше времени, см. рис 5.5. Отрезок на временной оси, не получивший своих точек-двойников на ломаной линии, определяет – насколько домосед будет старше путешественника при встрече.

Ситуация на рис. 5.5 несколько утрирована. Получается, что брат-путешественник стартовал с бесконечным ускорением, затем развернулся с бесконечным ускорением, и т. д. Реальная мировая линия брата-путешественника конечно плавная, соответствующая конечным ускорениям. Однако выводы не изменятся. Мы можем кривую аппроксимировать ломаной, причем с любой точностью. А анализ ломаной мировой линии, имеет она два отрезка, как на рис. 5.5, или любое другое количество отрезков, принципиально не отличается. Другими словами, парадокса не возникает, если не нарушаются правила вычисления интервалов. Тогда результат всегда таков: интервал отрезка aw на рис. 5.5 больше интервала, измеренного вдоль любой другой мировой линии, соединяющей события a и w . То есть собственное время домоседа всегда больше собственного времени любого путешественника из a в w .

Некоторые особенности ускоренных наблюдателей обсуждаются в Дополнении 6, которое лучше читать после главы 8 (о черных дырах).

В исторической литературе о науке много внимания уделяется взаимоотношениям создателей СТО в начале прошлого века. Иногда оценки разнятся чрезвычайно. К сожалению, часто доходят до крайностей, ничем не обоснованных. Можно было бы об этом просто не писать, но великие создатели великой теории тоже были людьми. Взаимоотношения были частью их жизни и, так или иначе, были связаны и с их творчеством.

Поскольку основными создателями СТО по праву считаются Пуанкаре и Эйнштейн, то на их взаимные отношения и отношение к ним научного сообщества обратим особое внимание. Весьма взвешанная оценка тех событий дана в послесловии (которое называется «Истоки релятивизма») в книге А. А. Тяпкина и А. С. Шабанова «Пуанкаре», вышедшей в 1979 году в серии «Жизнь замечательных людей». Поэтому, в основном, будем следовать изложению этого послесловия, иногда вставляя собственные комментарии. Но прежде, совсем немного об Анри Пуанкаре.

Математические таланты Пуанкаре проявились уже в престижной Политехнической школе. Там он опубликовал свою первую научную работу по дифференциальной геометрии. В 1875 году его приняли в еще более авторитетное заведение – Горную школу, где в 1879 году он защитил докторскую диссертацию, которая была оценена как «заслуживающая многих хороших диссертаций».

После этого Пуанкаре преподавал в нескольких университетах, иногда одновременно. Опубликовал несколько важных статей, фактически создавая новые разделы математики. Его исследования тесно связаны с небесной механикой и астрономией.

В 1887 году король Швеции Оскар II объявил математический конкурс и предложил участникам на выбор четыре темы. Самой сложной была первая: рассчитать совместное движение тел Солнечной системы. За нее и взялся Пуанкаре. Для решения этой проблемы, как минимум, необходимо было решить задачу совместного движения трех тел. Пуанкаре показал, что задача трех тел не имеет аналитического решения, но предложил эффективные методы приближенного решения. Эта работа и последовавшие за ней содержат идеи, ставшие базовыми для «теории хаоса».