Манжит Кумар - Квант. Эйнштейн, Бор и великий спор о природе реальности

4Пауль Эвальд, AHQP, интервью 8 мая 1962 года.

5 Enz (2002), p. 15.

6 Enz (2002), p. 9.

7 Pais (2000), p. 213.

8 Mehra and Rechenberg (1982), Vol. 1, Pt. 2, p. 378.

9Enz (2002), p. 49.

10 Cropper (2001), p. 257.

11Там же.

12Там же.

13 Mehra and Rechenberg (1982), Vol. 1, Pt. 2, p. 384.

14 Pauli (1946b), p. 27.

15 Mehra and Rechenberg (1982), Vol. 1, Pt. 1, p. 281.

16 CPAE, Vol. 8, p. 467. Письмо Эйнштейна Гедвиге Борн от 8 февраля 1918 года.

17 Greenspan (2005), p. 108.

18 Вот (2005), p. 56. Письмо Борна Эйнштейну от 21 октября 1921 года.

19 Pauli (1946а), p. 213.

20Там же.

21Лоренц предположил, что свет, который видел Зееман, испускают колеблющиеся электроны внутри атомов нагретого газообразного натрия. Лоренц показал, что в зависимости от того, наблюдается ли излученный свет в направлении параллельном или перпендикулярном магнитному полю, спектральные линии должны расщепляться на две (дуплет) или три (триплет) близколежащие линии. Он рассчитал разницу длин волн соседних линий и получил значение, согласующееся с экспериментальным результатом Зеемана.

22 Pais (1991), p. 199.

23 Pais (2000), p. 221.

24 Pauli (1946a), p. 213.

25В 1916 году двадцативосьмилетний немецкий физик Вальтер Коссель, отец которого был лауреатом Нобелевской премии по физиологии и медицине, первым установил связь между квантовыми свойствами атомов и периодической таблицей. Он обратил внимание, что разность между атомными номерами 2, 10 и 18 трех первых благородных газов (гелий, неон и аргон) равна 8. Коссель предположил, что электроны в таких атомах вращаются внутри “замкнутых оболочек”. Первая содержит два электрона, а вторая и третья — по восемь. Бор признавал важность работы Косселя, но ни Коссель, ни кто-либо другой не продвинулись так далеко, как датчанин, сумевший объяснить распределение электронов во всех атомах периодической таблицы. Венец работы Бора — правильное определение места гафния, который, как оказалось, не принадлежит к группе редкоземельных элементов.

26 BCW, Vol. 4, p. 740. Открытка, посланная Арнольдом Зоммерфельдом Бору, 7 марта 1921 года.

27 BCW, Vol. 4, p. 740. Письмо Арнольда Зоммерфельда Бору от 25 апреля 1921 года.

28 Pais (1991), p. 205.

29Если n = 3, то k = 1,2,3. Если k = 1, то m = 0, а энергетическое состояние есть (3,1,0). Если k = 2, то m = -1,0,1, а энергетические состояния суть (3,2, -1), (3,2,0) и (3,2,1). Если k = 3, то m = -2,-1,0,1,2, а энергетические состояния суть (3,3,-2), (3,3,-1), (3,3,0), (3,3,1) и (3,3,2). Полное число энергетических состояний третьей оболочки n = 3 равно 9, а максимальное число электронов —18. Для n = 4 энергетические состояния суть (4, 1,0), (4,2,-1), (4,2,0), (4,2,1), (4,3, -2), (4,3,-1), (4,3,0), (4,3,1) , (4,3,2), (4,4,-3), (4,4,-2), (4,4,-1), (4,4,0), (4,4,1), (4,4,2) и (4,4,3). Для данного значения n число электронных энергетических состояний равно n 2. Для первых четырех оболочек n = 1,2,3,4 числа электронных состояний суть 1,4,9,16.

30Первое издание Atombau und Spektrailinien опубликовано в 1919 году.

31 Pais (2000), p. 223.

32Проквантовав угловой момент, Бор ввел в модель атома квант. Угловым моментом обладает электрон, двигающийся по круговой орбите. Обозначим его буквой L. Угловой момент — произведение массы электрона на его скорость и на радиус орбиты ( L = mvr). Разрешены только те орбиты электронов, для которых угловой момент равен nh/2π . Остальные орбиты запрещены.

33 Calaprice (2005), p. 77.

34 Pais (1989b), p. 310.

35 Goudsmit (1976), p. 246.

36Сэмюэл Гаудсмит, AHQP, интервью 5 декабря 1963 года.

37 Pais (1989b), p. 310.

38 Pais (2000), p. 222.

39Эти два значения суть +1/2 ( h/2π ) и -1/2 ( h/2π ), или h/4π и -h/4π.

40 Mehra and Rechenberg (1982), Vol. 1, Pt. 2, p. 702.

41 Pais (1989b), p. 311.

42Джордж Уленбек, AHQP, интервью 31 марта 1962 года.

43 Uhlenbeck (1976), p. 253.

44 BCW, Vol. 5, p. 229. Письмо Бора Ральфу Кронигу от 26 марта 1926 года.

45 Pais (2000), p. 304.

46 Robertson (1979), p. 100.

47 Mehra and Rechenberg (1982), Vol. 1, Pt. 2, p. 691.

48 Mehra and Rechenberg (1982), Vol. 1, Pt. 2, p. 692.

49Ральф Крониг, AHQP, интервью 11 декабря 1962 года.

50 Там же.

51 Pais (2000), p. 305.

52Там же.

53Там же.

54Там же.

55 Uhlenbeck (1976), p. 250.

56 Pais (2000), p. 305.

57Там же.

58 Pais (2000), p. 230.

59 Enz (2002), p. 115.

60 Enz (2002), p. 117.

61 Goudsmit (1976), p. 248.

62 Jammer (1966), p. 196.

63 Mehra and Rechenberg (1982), Vol. 2, Pt. 2, p. 208. Письмо Паули Ральфу Кронигу от 21 мая 1925 года.

64 Mehra and Rechenberg (1982), Vol. 1, Pt. 2, p. 719.

1 Mehra and Rechenberg (1982), Vol. 2, p. 6.

2 Heisenberg (1971), p. 16.

3Там же.

4Там же.

5Там же.

6Вернер Гейзенберг, AHQP, интервью 30 ноября 1962 года.

7 Heisenberg (1971), p. 24.

8Там же.

9Вернер Гейзенберг, AHQP, интервью 30 ноября 1962 года.

10 Heisenberg (1971), p. 26.

11Там же.

12Там же.

13 Heisenberg (1971), p. 38.

14Там же.

15Вернер Гейзенберг, AHQP, интервью 30 ноября 1962 года.

16 Heisenberg (1971), p. 42.

17 Born (1978), p. 212.

18 Born (2005), p. 73. Письмо Борна Эйнштейну от 7 апреля 1923 года.

19 Воrn (1978), p. 212.

20 Cassidy (1992), p. 168.

21 Mehra and Rechenberg (1982), Vol. 2, pp. 140-141. Письмо Гейзенберга Паули от 26 марта 1924 года.

22 Mehra and Rechenberg (1982), Vol. 2, p. 133. Письмо Паули Бору от 11 февраля 1924 года.

23 Mehra and Rechenberg (1982), Vol. 2, p. 135. Письмо Паули Бору от 11 февраля 1924 года.

24 Mehra and Rechenberg (1982), Vol. 2, p. 142.

25 Mehra and Rechenberg (1982), Vol. 2, p. 127. Письмо Борна Бору от 16 апреля 1924 года.

26 Mehra and Rechenberg (1982), Vol. 2, p. 3.

27 Mehra and Rechenberg (1982), Vol. 2, p. 150.

28Фрэнк Хойт, AHQP , интервью 28 апреля 1964 года.

29 Mehra and Rechenberg (1982), Vol. 2, p. 209. Письмо Гейзенберга Бору от 21 апреля 1925 года.

30 Heisenberg (1971), p. 8.

31 Pais (1991), p. 270.

32 Mehra and Rechenberg (1982), Vol. 2, p. 196. Письмо Паули Бору от 12 декабря 1924 года.

33 Cassidy (1992), p. 198.

34 Pais (1991), p. 275.

35 Heisenberg (1971), p. 60.

36Там же.

37 Heisenberg (1971), p. 61.

38Там же.

39Там же.

40

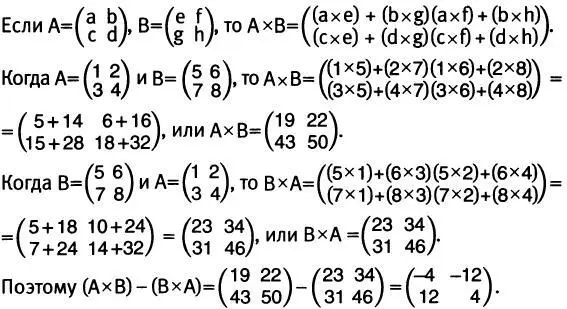
41 Enz (2002), p. 131. Письмо Гейзенберга Паули от 21 июня 1925 года.

42 Cassidy (1992), p. 197. Письмо Гейзенберга Паули от 9 июля 1925 года.

43 Mehra and Rechenberg (1982), p. 291.

44 Enz (2002), p. 133.

45 Cassidy (1992), p. 204.

46 Heisenberg (1925), p. 276.

47 Born (2005), p. 82. Письмо Борна Эйнштейну от 15 июля 1925 года. Вполне возможно, что к тому времени, когда Борн написал Эйнштейну, он уже понял, что правило умножения Гейзенберга полностью совпадает с правилом умножения матриц. Борн утверждал, что Гейзенберг дал ему свою статью 11 или 12 июля. Однако в другой раз он говорил, что установил тождество странного правила умножения с правилом умножения матриц 10 июля.

48 Воrn (2005), p. 82. Письмо Борна Эйнштейну от 15 июля 1925 года.

49 Cropper (2001), p. 269.

50 Born (1978), p. 218.

51 Schweber (1994), p. 7.

52 Воrn (2005), p. 80. Письмо Борна Эйнштейну от 15 июля 1925 года.

53В 1925-1926 годах ни Гейзенберг, ни Борн, ни Йордан не использовали термин “матричная механика”. Они говорили “новая механика” либо “квантовая механика”. Остальные ссылались на нее как на “механику Гейзенберга” или “геттингенскую механику”, пока кто-то из математиков не назвал ее Matrizenphysik — “матричная физика”. Гейзенбергу это название никогда не нравилось.