Ричард Фейнман - 8. Квантовая механика I

Мы собираемся все расчеты вести нерелятивистски, так что именно таким видом амплитуд вероятностей мы и будем поль­зоваться.

Заметьте, что наше релятивистское преобразование снаб­дило нас формулой для изменения амплитуды атома, движу­щегося в пространстве, не требуя каких-либо добавочных до­пущений. Волновое число ее изменений в пространстве, как это следует из (5.9), равно

а, значит, длина волны

Это та самая длина волны, которую мы раньше использовали для частиц с импульсом р. Именно таким путем де-Бройль впервые пришел к этой формуле. Для движущейся частицы частота изменения амплитуды по-прежнему дается формулой

Абсолютная величина (5.9) равна просто единице, так что для частицы, движущейся с определенной энергией, вероят­ность обнаружить ее где бы то ни было - одна и та же повсю­ду и со временем не меняется. (Важно отметить, что амплиту­да это комплексная волна. Если бы мы пользовались веще­ственной синусоидой, то ее квадрат от точки к точке менялся бы, что было бы неверно.)

Конечно, мы знаем, что бывают случаи, когда частицы дви­жутся от одного места к другому, так что вероятность зависит от положения и изменяется со временем. Как же нужно опи­сывать такие случаи? Это можно сделать, рассматривая ампли­туды, являющиеся суперпозицией двух или большего числа амплитуд для состояний с определенной энергией. Такое поло­жение мы уже обсуждали в гл. 48 (вып. 4), причем именно для амплитуд вероятности! Мы нашли тогда, что сумма двух ам­плитуд с разными волновыми числами k (т. е. импульсами) и частотами w (т. е. энергиями) приводит к интерференционным буграм, или биениям, так что квадрат амплитуды меняется и в пространстве, и во времени. Мы нашли также, что эти биения движутся с так называемой «групповой скоростью», опреде­ляемой формулой

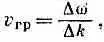
где Dk и Dw — разности волновых чисел и частот двух волн. В более сложных волнах, составленных из суммы многих амплитуд с близкими частотами, групповая скорость равна

Так как w =Е р /h, a k = p/h, то

Но из (5.6) следует, что

а так как E p =Mc 2 , то

а это как раз классическая скорость частицы. Даже применяя нерелятивистские выражения, мы будем иметь

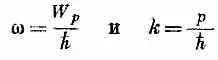
и

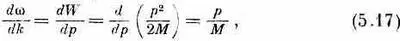
т. е. опять классическую скорость.

Результат наш, следовательно, состоит в том, что если име­ется несколько амплитуд для чистых энергетических состоянии с почти одинаковой энергией, то их интерференция приводит к «всплескам» вероятности, которые движутся сквозь прост­ранство со скоростью, равной скорости классической частицы с такой же энергией. Но нужно, однако, заметить, что, когда мы говорим, что можем складывать две амплитуды с разными волновыми числами, чтобы получать пакеты, отвечающие дви­жущейся частице, мы при этом вносим нечто новое — нечто, не выводимое из теории относительности. Мы сказали, как ме­няется амплитуда у неподвижной частицы, и затем вывели из этого, как она должна была бы меняться, если бы частица двигалась. Но из этих рассуждений мы не в состоянии вывести, что случилось бы, если бы были две волны, движущиеся с раз­ными скоростями. Если мы остановим одну из них, мы не смо­жем остановить другую. Так что мы втихомолку добавили еще одну гипотезу: кроме того, что (5.9) есть возможное реше­ние, мы. допускаем, что у той же системы могут быть еще ре­шения со всевозможными p и что различные члены будут интерферировать.

§ 3. Пoтeнциальная энергия; сохранение энергии

А теперь мы хотели бы выяснить вопрос о том, что бывает; когда энергия частицы может меняться. Начнем с размышления о частице, которая движется в поле сил, описываемом потен­циалом. Рассмотрим сперва влияние постоянного потенциала. Пусть у нас имеется большой металлический ящик, который мы зарядили до некоторого электростатического потенциала j (фиг. 5.2).

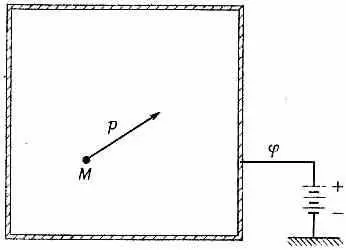
|Фиг. 5.2. Частица с массой M и импульсом р в области постоянного потенциала.

Если внутри ящика есть заряженные объекты, то их потенциальная энергия будет равна q j; мы обозначим это число буквой V. Оно по условию совершенно не зависит от положения самого объекта. От наложения потенциала никаких физических изменений внутри ящика не произойдет, ведь постоянный потенциал ничего не меняет в том, что происходит внутри ящика. Значит, закон, по которому теперь будет меняться амплитуда, вывести никак нельзя. Можно только догадаться. Вот он, правильный ответ — он выглядит примерно так, как и следовало ожидать: вместо энергии нужно поставить сумму потенциальной энергии V и энергии Е р , которая сама есть сумма внутренней и кинетической энергий. Амплитуда тогда будет пропорциональна

Общий принцип состоит в том, что коэффициент при t, который можно было бы назвать со, всегда дается полной энергией системы: внутренней энергией («энергией массы») плюс кине­тическая энергия плюс потенциальная энергия:

Или в нерелятивистском случае

Ну, а что можно сказать о физических явлениях внутри ящика? Если физическое состояние не одно, а несколько, то что мы получим? В амплитуду каждого состояния войдет один и тот же добавочный множитель