Ричард Фейнман - 8. Квантовая механика I

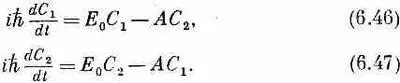
Эти уравнения достаточно просты и могут быть решены разным путем. Удобно решать их так. Складывая их, по­лучаем

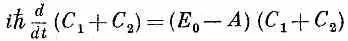
с решением

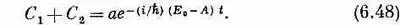
Вычитая затем (6.47) из (6.46), получаем

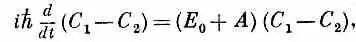
что дает

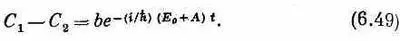
Две постоянные интегрирования мы обозначили а и b; их надо выбрать так, чтобы получились подходящие начальные условия данной физической задачи. Наконец, складывая и вычитая (6.48) и (6.49), получаем C 1и С 2:

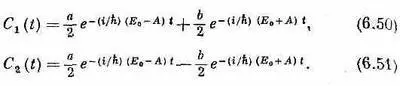
Они отличаются только знаком при втором слагаемом.

Решения-то мы получили, но что они значат? (В квантовой механике трудность не только в том, чтобы получить решения но и в том, чтобы разобраться в их смысле!) Заметьте, что при b= 0оба решения обладают одинаковой частотой w =(E 0 -A)/h Если все меняется с одной частотой, это значит, что система пребывает в состоянии с определенной энергией, в данном слу­чае с энергией (Е 0 -А). Значит, существует стационарное состояние с такой энергией; в нем обе амплитуды С 1и C 2равны друг другу. Мы приходим к выводу, что молекула аммиака обладает определенной энергией (Е 0 - А), если для атома азота одинакова амплитуда оказаться «вверху» и «внизу».

Имеется другое допустимое стационарное состояние, когда а=0; тогда обе амплитуды обладают частотой (E 0 +A)/h. Зна­чит, имеется другое состояние с определенной энергией (Е 0 +А), когда две амплитуды равны, но отличаются знаком: C 2 =-C 1 . Вот и все состояния с определенной энергией. В следующей главе мы поговорим о состояниях молекулы аммиака подроб­нее; здесь же мы отметим еще только некоторые особенности.

Мы приходим к заключению, что из-за того, что имеется некоторая вероятность перескока атома азота из одного по­ложения в другое, энергия молекулы равна не просто Е 0 , как можно было ожидать, но обладает двумя энергетическими уровнями ( Е 0 +А )и ( Е 0 -А ) . Каждое из возможных состояний молекулы, какую бы энергию оно ни имело, «расщепляется» на два уровня. Мы говорим «каждое из состояний», потому что, как вы помните, мы выбрали какое-то определенное состояние вращения с определенной внутренней энергией и т. д. И для каждых мыслимых условий подобного рода возникает (из-за возможности переворота молекулы) пара энергетических уров­ней.

Теперь поставим следующий вопрос. Пусть мы знаем, что при t= 0молекула находится в состоянии | 1>, т. е. что С 1{0)=1 и С 2(0)=0. Какова вероятность того, что молекула будет обна­ружена в момент t в состоянии |2> или же что она окажется в этот момент в состоянии |1>? Наши начальные условия го­ворят нам, какими должны быть а и b в (6.50) и (6.51). Полагая t=0, имеем

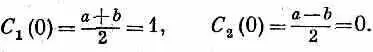
Значит, а = b =1. Подставляя их в формулы для С 1 (t) и С 2 (t) и вынося общий множитель, получаем

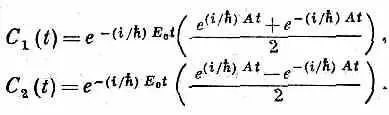
Это можно переписать так:

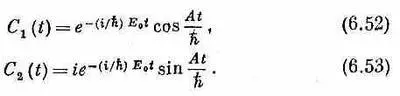
Величина обеих амплитуд гармонически изменяется во времени. Вероятность того, что молекула будет обнаружена в со­стоянии |2> в момент t, равна квадрату модуля C 2 (t):

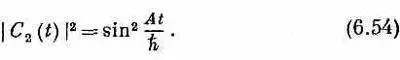
Она, как и следует, начинается с нуля, растет до единицы и затем колеблется вперед и назад между нулем и единицей, как показано на кривой, обозначенной P 2, на фиг. 6.2.

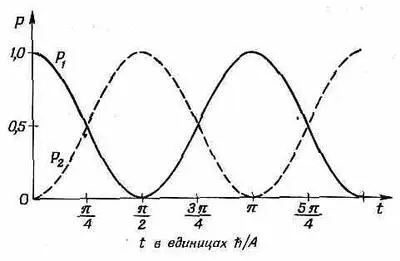
Фиг. 6.2. p 1 — вероятность того, что молекула аммиака, находившаяся при t=0 в состоянии |1>, бу­дет обнаружена в момент t тоже в состоянии |1>; Р 2 — вероятность того, что она будет обнаружена в состоянии |2>.

Вероят­ность остаться в состоянии |1> тоже, конечно, не остается равной единице. Она «перекачивается» во второе состояние до тех пор, пока вероятность увидать молекулу в первом состоя­нии не обратится в нуль, как показано на кривой Р 1фиг. 6.2. Вероятность попросту переливается туда и обратно между этими двумя состояниями.

Еще раньше мы видели, что бывает, если качаются два одинаковых маятника, слегка связанные друг с другом [см. гл.49 (вып.4)]. Когда мы отводим в сторону один из них и отпускаем, он колеблется, но затем постепенно начинает колебаться дру­гой и вскоре забирает себе всю энергию. Затем процесс обра­щается, и энергию отбирает первый маятник. В точности то же самое происходит и здесь. Скорость, с какой происходит обмен энергией (быстрота просачивания «колебаний»), зависит от связи между маятниками. Кроме того, как вы помните, при двух маятниках существуют два определенных типа движений (каждый с определенной частотой), которые мы назвали фун­даментальными типами колебаний. Если отклонить оба маят­ника вместе, они колеблются с одной частотой. Если же отклонить один в одну сторону, а другой — в другую, то появляется иной стационарный тип колебаний и тоже с определенной частотой. С тем же мы встретились и сейчас — молекула аммиака математически походит на пару маятников. Существуют две частоты (E 0 +A)/h и (Е 0 -A)/h, при которых они колеблются либо разом, либо навстречу друг другу.

Сходство с маятником ненамного глубже принципа, что у оди­наковых уравнений и решения одинаковы. Линейные уравнения для амплитуд (6.39) очень похожи на линейные уравнения для гармонических осцилляторов. (В действительности именно этой причине обязана успехом наша классическая теория пока­зателя преломления, в которой квантовомеханический атом мы заменяли гармоническим осциллятором, хотя классически неразумно говорить об электронах, циркулирующих вокруг ядра.) Толкнув атом азота в одну сторону, вы получите супер­позицию этих двух колебаний и тем самым своеобразные бие­ния, потому что система не будет находиться в том или ином состоянии с определенной частотой. Однако расщепление уров­ней энергии молекулы аммиака — это строго квантовомеханический эффект.