Ричард Фейнман - 7. Физика сплошных сред

Поэтому для ядер обычно пишут (в скобках положительная величина)

m =g(q e /2m p ) J (34.7)

где m p — масса протона, а постоянная g, называемая ядерным g-фактором,— число порядка единицы, которое должно опре­деляться отдельно для каждого сорта ядер.

Другое важное отличие в случае ядер состоит в том, что g-фактор спинового магнитного момента протона не равен 2, как у электрона. Для протона g=2·(2,79). Крайне удивительно, что спиновый магнитный момент есть и у нейтрона и отношение этого магнитного момента к моменту количества движения равно 2·(-1,93). Другими словами, нейтрон в магнитном смысле не будет в точности «нейтральным». Он напоминает маленький маг­нитик и имеет такой же магнитный момент, как и вращающийся отрицательный заряд.

§ 3. Прецессия атомных магнитиков

Одно из следствий пропорциональности магнитного момента моменту количества движения заключается в том, что атомные магнитики, помещенные в магнитное поле, будут прецессироватъ. Обсудим это сначала с точки зрения классической физики. Пусть у нас имеется магнитный момент m , свободно висящий в однородном магнитном поле. Он испытывает действие момента силы t, равного mX B, пытающегося повернуть его в том же направлении, что и поле. Но атомный магнит — ведь это гиро­скоп, у него есть момент количества движения J. Поэтому момент силы от магнитного поля не вызовет поворота в направлении поля. Вместо этого магнит, какмы видели, когда говорили о гироскопе в гл. 20 (вып. 2), начнет првцессироватъ. Момент количества движения, а вместе с ним и магнитный момент прецессируют вокруг оси, параллельной магнитному полю. Скорость прецессии можно найти тем же мето­дом, что и в гл. 20 (вып. 2).

Предположим, что за малый промежуток времени Dt момент количества движения меняется от Jдо J' (фиг. 34.3), оставаясь при этом всегда под одним и тем же углом q к направлению маг­нитного поля В.

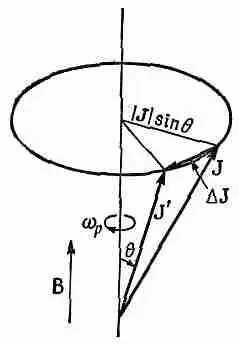
Фиг. 34.3. Объект в моментом количества движения J и параллельным ему магнитным моментом m в магнитном поле В прецессирует с угловой скоростью w p ,.

Обозначим через w pугловую скорость прецес­сии, так что за промежуток времени Dt угол прецессии будет равен w pDt. Из геометрии рисунка мы видим, что изменение момента количества движения за время Dt равно

DJ=(Jsinq)(w pDt), а скорость изменения момента количества движения

dJ/dt=w p Jsinq (34.8)

что должно равняться моменту силы

t=mBsinq. (34.9)

Угловая скорость прецессии будет равна

Подставляя из уравнения (34.6) отношение m/ J, мы видим, что для атомной системы

w p=g(q e/2m)B (34.11)

т. е. частота прецессии пропорциональна В. Полезно запом­нить, что для атома (или электрона)

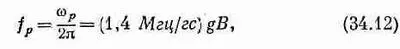
а для ядра

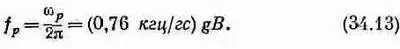
(Формулы для атомов и ядер различны только благодаря раз­личным соглашениям относительно g в этих двух случаях.) Итак, в соответствии с классической теорией электронные ор­биты и спины в атоме должны прецессировать в магнитном поле. Верно ли это и в квантовой механике? В сущности это верно, однако смысл «прецессии» здесь совсем иной. В квантовой механике нельзя говорить о направлении момента количества движения в том же смысле, как это делается классически; тем не менее аналогия здесь очень близкая, настолько близкая, что мы продолжаем пользоваться термином «прецессия». Мы еще обсудим это позднее, когда будем говорить о квантовомеханической точке зрения.

§ 4. Диамагнетизм

Рассмотрим теперь с классической точки зрения диамагнетизм. К этому можно подойти несколькими путями, но один из лучших такой. Предположим, что по соседству с атомом мед­ленно включается магнитное поле. При изменении магнитного поля благодаря магнитной индукции будет генерироваться электрическое поле. По закону Фарадея контурный интеграл от Епо замкнутому контуру равен скорости изменения магнит­ного потока через этот контур. Предположим, что в качестве контура Г мы выбрали окружность радиусом r, центр которой совпадает с центром атома (фиг. 34.4).

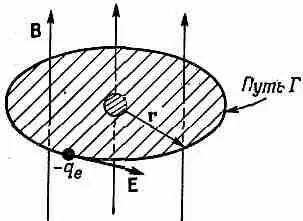
Фиг. 34.4. Индуцированные элект­рические силы, действующие на элект­роны в атоме.

Среднее тангенциальное электрическое поле Е на этом контуре определяется выраже­нием

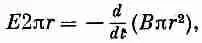
т. е. возникает циркулирующее электрическое поле, напряжен­ность которого равна

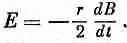
Индуцированное электрическое поле, действуя на атомный электрон, создает момент силы, равный -q eEr , который дол­жен быть равен скорости изменения момента количества дви­жения dJ/dt:

Интегрируя теперь по времени, начиная с нулевого поля, мы находим, что изменение момента количества движения из-за включения поля будет равно

Это и есть тот дополнительный момент количества движения, который сообщается электрону за время включения поля.

Такой добавочный момент количества движения приводит к добавочному магнитному моменту, который благодаря тому, что это орбитальное движение, равен просто произведению - q e /2m на момент количества движения. Наведенный диамаг­нитный момент

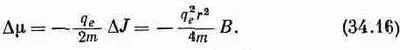
Знак минус (как можно убедиться непосредственно из закона Ленца) означает, что направление добавочного момента проти­воположно магнитному полю.