Ричард Фейнман - 7. Физика сплошных сред

Фиг. 41.1. Увлечение жидкости между двумя параллельными пластинками.

Если вы будете измерять силу, требуемую для поддержания движения верхней пластины, то найдете, что она пропорциональна площади пластины и отно­шению v 0 /d, где d — расстояние между пластинами. Таким образом, напряжение сдвига F/A пропорционально v 0 /d:

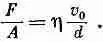
Коэффициент пропорциональности h называется коэффициен­том вязкости.

Если перед нами более сложный случай, то мы всегда можем рассмотреть в воде небольшой плоский прямоугольный объем, грани которого параллельны потоку (фиг. 41.2).

Фиг. 41.2. Напряжения сдви­га в вязкой жидкости.

Силы в этом объеме определяются выражением

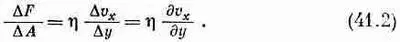
Далее, дv x /дy представляет скорость изменения деформаций сдвига, определенных нами в гл. 38, так что силы в жидкости пропорциональны скорости изменения деформаций сдвига.

В общем случае мы пишем

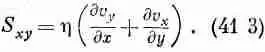
При равномерном вра­щении жидкости производ­ная дu х /ду равна дv y /дx с обратным знаком, a S xy будет равна нулю, как это и требуется, ибо в равно­мерно вращающейся жидкости напряжения отсутствуют. (Подобную же вещь мы проде­лывали в гл. 39 при определении е xy .) Разумеется, для S yz и S гх тоже есть соответствующие выражения.

В качестве примера применения этих идей рассмотрим дви­жение жидкости между двумя коаксиальными цилиндрами. Пусть радиус внутреннего цилиндра равен а, его скорость будет v а, а радиус внешнего цилиндра пусть будет b , а скорость равна v b (фиг. 41.3).

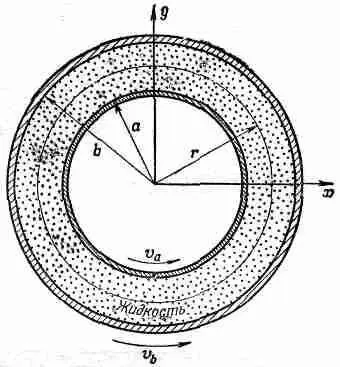
Фиг. 41.3. Поток жидкости между двумя концентрическими цилиндрами, вращающимися с разными угловыми скоростями.

Возникает вопрос, каково распределение скоростей между цилиндрами? Чтобы ответить на него, начнем с получения формулы для вязкого сдвига в жидкости на рас­стоянии r от оси. Из симметрии задачи можно предположить, что поток всегда тангенциален и что его величина зависит только от r ; v=v(r). Если мы понаблюдаем за соринкой в воде, расположенной на расстоянии r от оси, то ее координаты как функции времени будут

x = rcoswt, у=r sinwt,

где w= v/r. При этом х- и y-компоненты скорости равны

v x =- rwsinwt =-w у и v y = rwcoswt=w х. (41.4)

Из формулы (41.3) получаем

Для точек с у= 0 имеем д w /ду =0, а х(д w /дх) будет равно r (d w )/dr). Так что в этих точках

(Разумно думать, что величина S должна зависеть от дw/дr, когда w не изменяется с r, жидкость находится в состоянии равномерного вращения и напряжения в ней не возникают.) Вычисленное нами напряжение представляет собой танген­циальный сдвиг, одинаковый повсюду вокруг цилиндра. Мы можем получить момент сил, действующий на цилиндриче­ской поверхности радиусом r, путем умножения напряжения сдвига на плечо импульса r и площадь 2prl:

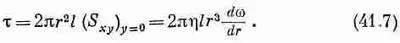
Поскольку движение воды стационарно и угловое уско­рение отсутствует, то полный момент, действующий на ци­линдрическую поверхность воды между радиусами r и r+ dr, должен быть нулем; иначе говоря, момент сил на расстоянии r должен уравновешиваться равным ему и противоположно на­правленным моментом сил на расстоянии r+ dr, так что t не должно зависеть от r . Другими словами, r 3(dw/dr) равно некоторой постоянной, скажем А, и

dw/dr=A/r 3(41.8)

Интегрируя, находим как w изменяется с r:

Постоянные А и В должны определяться из условия, что w=w aв точке r=a , a w=w bв точке r=b. Тогда находим

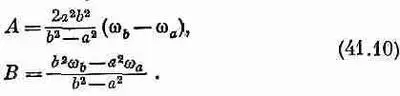
Таким образом, w как функция r нам известна, а стало быть, известно и v=wr .

Если же нам нужно определить момент сил, то его можно получить из выражений (41.7) и (41.8);

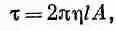
или

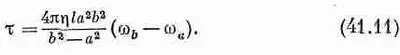
Он пропорционален относительной угловой скорости двух цилиндров. Имеется стандартный прибор для измерения коэф­фициентов вязкости, который устроен следующим образом: один из цилиндров (скажем, внешний) посажен на ось, но удер­живается в неподвижном состоянии пружинным динамометром, который измеряет действующий на него момент сил, а внутрен­ний цилиндр вращается с постоянной угловой скоростью. Коэффициент вязкости определяется при этом из формулы (41.11).

Из определения коэффициента вязкости вы видите, что h измеряется в ньютон · сек/м 2 . Для воды при 20° С

h=10 3 нъютон · сек/м 2 .

Часто удобнее бывает пользоваться удельной вязкостью, которая равна h, деленной на плотность r. При этом величины удельных вязкостей воды и воздуха сравнимы:

Вода при 20°С h/r=10 - 6 м 2 /сек

Воздух при 20°С h/r=15·10 - 6м 2/сек. , (41.12)

Обычно вязкость очень сильно зависит от температуры. Напри­мер, для воды непосредственно над точкой замерзания отно­шение h/r в 1,8 больше, чем при 20° С.

§ 2. Вязкий поток

Перейдем теперь к общей теории вязкого потока, по крайней мере настолько общей, насколько это и известно человеку. Вы уже понимаете, что компоненты сдвиговых напряжений сдвига пропорциональны пространственным производным от раз­личных компонент скорости, таких, как dv x /dy или dv y /дх. Однако в общем случае сжимаемой жидкости в напряжениях есть и другой член, который зависит от других производных скорости. Общее выражение имеет вид