Ричард Фейнман - 6a. Электродинамика

Начнем с прямоугольной трубы, ее проще всего анализи­ровать. Сперва изложим все математически, а потом еще раз вернемся назад и рассмотрим вопрос более элементарно. Но этот более элементарный подход легко применить лишь к прямо­угольным трубам. Основные же явления в любой трубе одни и те же, так что математические доводы звучат более основа­тельно.

Поставим перед собой следующий вопрос: какого типа волны могут существовать в прямоугольной трубе? Выберем сначала удобные оси координат: ось z направим вдоль трубы, а оси х и у — вдоль стенок (фиг. 24.3).

Известно, что когда волны света бегут по трубе, их электри­ческое поле поперечно; поэтому начнем с поиска таких решений, в которых Е перпендикулярно z, скажем решений с одной толь­ко y-компонентой Е y(фиг. 24.4,а). Это электрическое поле должно как-то меняться поперек волновода; действительно, ведь оно должно обратиться в нуль на сторонах, параллельных оси у: токи и заряды в проводнике устраиваются всегда так, чтобы на его поверхности не осталось никаких касательных составляющих электрического поля.

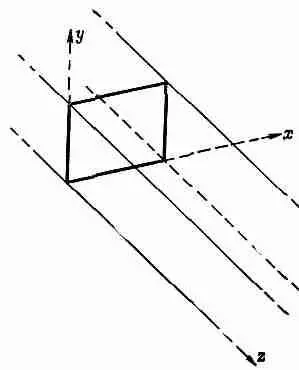
Фиг, 24.3. Выбор осей коорди­нат для прямоугольного волно­вода.

Значит, график Е yот х должен напоминать некоторую дугу (фиг. 24.4,6). Может быть, это найденная нами для полости функция Бесселя? Нет, функции Бесселя появляются только в задачах с цилиндрической сим­метрией. При прямоугольных сечениях волны — это обычные гармонические функции, что-нибудь вроде sink xx.

Раз мы ищем волны, которые бегут вдоль трубы, то следует ожидать, что поле как функция z будет колебаться между по­ложительными и отрицательными значениями (фиг. 24.5) и что должно как-то меняться поперек волновода; действительно, ведь оно должно обратиться в нуль на сторонах, параллельных оси у: токи и заряды в проводнике устраиваются всегда так, чтобы на его поверхности не осталось никаких касательных составляющих электрического поля.

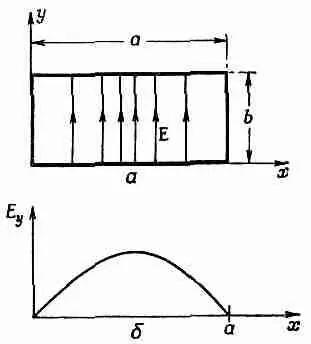
Фиг. 24.4. Электрическое поле в волноводе при некотором зна­чении z.

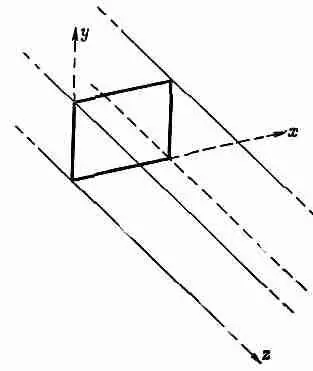
Фиг. 24.3. Выбор осей коорди­нат для прямоугольного волно­вода.

Значит, график Е yот х должен напоминать некоторую дугу (фиг. 24.4,6). Может быть, это найденная нами для полости функция Бесселя? Нет, функции Бесселя появляются только в задачах с цилиндрической сим­метрией. При прямоугольных сечениях волны — это обычные гармонические функции, что-нибудь вроде sink xx.

Раз мы ищем волны, которые бегут вдоль трубы, то следует ожидать, что поле как функция z будет колебаться между по­ложительными и отрицательными значениями (фиг. 24.5) и что

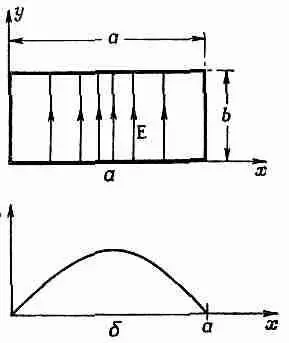
Фиг. 24,4. Электрическое поле в волноводе при некотором зна­чении z.

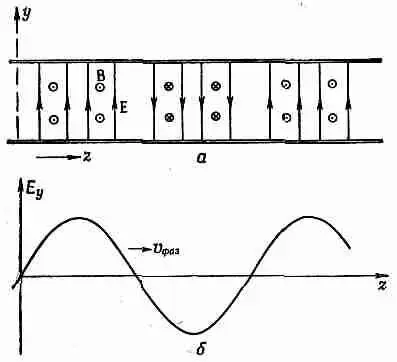
Фиг. 24.5. Зависимость поля в волноводе от z.

эти колебания будут бежать вдоль трубы с какой-то скоростью v. Если имеются колебания с определенной частотой w, то надо испытать, может ли волна меняться по z как cos(wt—k zz) или, в более удобной математической форме, как е i(wt-k 2z). Такая зависимость от z представляет волну, бегущую со скоростью v=w/k z[см. гл. 29 (вып. 3)].

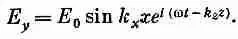
Значит, можно допустить, что волна в трубе имеет следую­щую математическую форму:

(24.12)

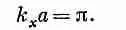
Давайте-ка поглядим, можно ли при таком допущении удов­летворить правильным уравнениям поля. Во-первых, электри­ческое поле не должно иметь составляющих, касательных к про­воднику. Для этого наше поле подходит; вверху и внизу оно на­правлено поперек стенок, а с боков равно нулю. Впрочем, для последнего необходимо, чтобы полволны sin k xx как раз укла­дывалось на всей ширине волновода, т. е. чтобы было

(24.13)

Это условие определяет k x . Есть и иные возможности, например k x a=2p, З p , ... или в общем случае

(24.14)

где n — целое. Все они представляют различные сложные рас­положения полей, но мы дальше будем говорить о самом прос­том, когда k x=p/a, a a — внутренняя ширина трубы.

Далее, дивергенция Е в пустом пространстве внутри трубы должна быть равна нулю, потому что в трубе нет зарядов. У нашего Е есть только y-компонента, но по у она не меняется, так что действительно V·Е=0.

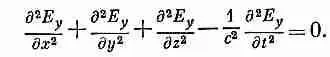
Наконец, наше электрическое поле должно согласовываться с остальными уравнениями Максвелла для пустого пространст­ва внутри трубы. Это все равно, что потребовать, чтобы оно удовлетворяло волновому уравнению

(24.15)

Нам надо проверить, подойдет ли сюда выбранная нами форма (24.12). Вторая производная Е yпо х просто равна —k 2 хЕ у. Вторая производная по у равна нулю, потому что от у ничего не зависит. Вторая производная по z есть —k 2 zE y, а вторая про­изводная по t это —w 2Е y. Тогда уравнение (24.15) утверждает, что

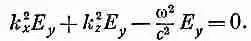
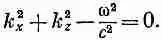
Если Е y не обращается всюду в нуль (этот случай нас не очень интересует), то это уравнение выполняется всегда, если

(24.16)

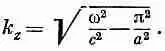
Число k x мы уже закрепили, так что это уравнение говорит нам, что волны предположенного нами типа возможны лишь тогда, когда k z связано с частотой w условием (24.16), т. е. когда

(24.17)

Волны, которые мы описали, распространяются в направлении z с таким значением k z .

Волновое число k z, которое мы получили из (24.17), дает нам при данной частоте w скорость, с которой бегут вдоль трубы узлы волны. Фазовая скорость равна

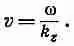
(24.18)

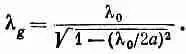
Вспомните теперь, что длина l, бегущей волны дается форму­лой l =2pv/ w , так что k z также равняется 2p/ l g , где l g — длина волны осцилляции в направлении z — «длина волны в волново­де». Длина волны в волноводе, конечно, отличается от длины электромагнитных волн той же частоты, но в пустом простран­стве. Если длину волны в пустом пространстве обозначить l 0(что равно 2 p с/w), то (24.17) можно переписать в таком виде: