Ричард Фейнман - 6. Электродинамика

§ 4. Парадокс

Теперь мы хотели бы предложить вам некий кажущийся парадокс. Парадокс возникает тогда, когда при одном способе рассуждений получается один ответ, а при другом способе — совсем другой, так что мы остаемся в неведении, что же собст­венно должно быть на самом деле. Разумеется, в физике никогда не бывает настоящих парадоксов, потому что существует только один правильный ответ; по крайней мере мы верим, что природа поступает только единственным способом (и именно этот спо­соб, конечно, правильный). Поэтому в физике парадокс — всего лишь путаница в нашем собственном понимании. Итак, вот наш : парадокс.

Представим, что мы конструируем прибор (фиг. 17.5), в котором имеется тонкий круглый пластмассовый диск, ук­репленный концентрически на оси с хорошими подшипниками, так что он совершенно свободно вращается. На диске имеется катушка из проволоки — короткий соленоид, концентричный по отношению к оси вращения. Через этот соленоид проходит постоянный ток / от маленькой батареи, также укрепленной на диске. Вблизи края диска по окружности на равном расстоянии размещены маленькие металлические шарики, изолированные друг от друга и от соленоида пластмассовым материалом диска. Каждый из этих проводящих шариков заряжен одинаковым зарядом Q. Вся картина стационарна, и диск неподвижен. Предположим, что случайно, а может и намеренно, ток в соленоиде прекратился, но, разумеется, без какого-либо вмешательства извне. Пока через соленоид шел ток, более или менее параллельно оси диска проходил магнитный поток.

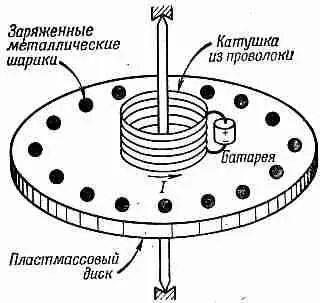
Фиг. 17.5. Повернется ли диск, если ток I прекратится?

После того как ток прервался, поток этот должен уменьшиться до нуля. Поэтому должно возникать индуцированное электрическое поле, которое будет циркулировать по окружностям с центром на оси диска. Заряженные шарики на периферии диска будут все испытывать действие электрического поля, касательного к внеш­ней окружности диска. Эта электрическая сила направлена для всех зарядов одинаково и, следовательно, вызовет у диска вра­щающий момент. Из этих соображений можно ожидать, что, когда ток в соленоиде исчезнет, диск начнет вращаться. Если нам известны момент инерции диска, ток в соленоиде и заряд шариков, то можно вычислить результирующую угловую

скорость.

Но можно рассуждать и по-другому. Используя закон сох­ранения момента количества движения, мы могли бы сказать, что момент диска со всеми его пристройками вначале равен нулю, поэтому момент всей системы должен оставаться нуле­вым. Никакого вращения при остановке тока быть не должно. Какое из доказательств правильно? Повернется ли диск или нет? Мы предлагаем вам подумать над этим вопросом.

Хотелось бы предостеречь вас, что правильный ответ не за­висит от всяких несущественных факторов, таких, как несим­метричное положение батареи, например. В самом деле, вы можете представить себе, скажем, такой идеальный случай: соленоид сделан из сверхпроводящей проволоки, через которую проходит ток. После того как диск тщательно установлен неподвижным, температуру соленоида медленно начинают повышать. Когда температура проволоки достигнет переход­ного значения между сверхпроводимостью и нормальной прово­димостью, ток в соленоиде обратится в нуль вследствие сопро­тивления проволоки. Поток, как и раньше, упадет до нуля и вокруг оси возникнет электрическое поле. Мы хотели бы также предостеречь вас, что решение не простое, но это и не обман. Когда вы разберетесь в этом, вы обнаружите важный закон электромагнетизма.

§ 5. Генератор переменного тока

В оставшейся части этой главы мы применим принципы, из­ложенные в § 1 для анализа ряда явлений, обсуждавшихся в гл. 16. Сначала мы рассмотрим подробно генератор перемен­ного тока. Такой генератор в основном состоит из проволочной катушки, вращающейся в однородном магнитном поле. Тот же самый результат может быть достигнут с помощью неподвиж­ной катушки в магнитном поле, направление которого вращает­ся по способу, описанному в предыдущей главе. Мы рассмотрим лишь первый случай. Пусть имеется круглая катушка из про­волоки, которая может вращаться вокруг оси, проходящей вдоль одного из ее диаметров. И пусть эта катушка помещена в магнитное поле, перпендикулярное оси вращения (фиг. 17.6). Представим себе, что оба конца катушки выведены на внешнюю цепь с помощью каких-нибудь скользящих контактов.

Благодаря вращению катушки магнитный поток через нее будет меняться. Поэтому в цепи катушки появится э. д. с. Пусть S —- площадь катушки, а q — угол между магнитным полем и нормалью к плоскости катушки. Тогда поток через катушку равен

BScosq. (17.13)

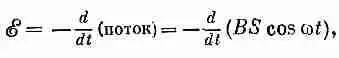
Если катушка вращается с постоянной угловой скоростью w, то q меняется со временем как wt. Тогда э. д. с. о в ка­тушке равна

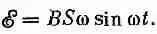
или

(17.14)

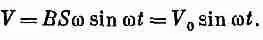
Если мы выведем провода из генератора на некоторое рас­стояние от вращающейся катушки, в место, где магнитное поле равно нулю или хотя бы не меняется со временем, то ротор от Е в этой области будет равен нулю, и мы сможем определить электрический потенциал. В самом деле, если ток не уходит из генератора, то разность потенциалов V между двумя прово­дами будет равна э. д. с. вращающейся катушки, т. е.

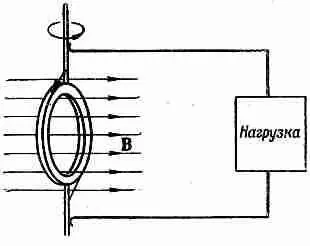
Фиг. 17.6. Катушка из проволоки, вращающаяся в однородном маг­нитном поле, — основная идея ге­нератора переменного тока.

Разность потенциалов в проводах меняется как sinwt. Такая меняющаяся разность потенциалов называется переменным напряжением.

Поскольку между проводами имеется электрическое поле, они должны быть электрически заряжены. Ясно, что э. д. с. генератора выталкивает лишние заряды в провода, пока их электрическое поле не становится достаточно сильным, чтобы в точности уравновесить силу индукции. Если посмотреть на генератор со стороны, то покажется, будто два провода электро­статически заряжены до разности потенциалов V, а заряды как бы меняются со временем, создавая переменную разность потенциалов. Есть и еще одно отличие от того, что наблюдается в случае электростатики. Если присоединить генератор к внеш­ней цепи, по которой может проходить ток, мы обнаружим, что э. д. с. не позволяет проводам разряжаться, а продолжает подпитывать их зарядами, когда из них уходит ток, стремясь сохранить на проводах одну и ту же разность потенциалов. Если генератор подключен к цепи, полное сопротивление которой равно R, ток в цепи будет пропорционален э. д. с. генератора и обратно пропорционален R. Поскольку э. д. с. синусои­дально изменяется со временем,