Ричард Фейнман - 5b. Электричество и магнетизм

Мы можем оценить сумму, проинтегрировав по угловому распределению. Телесный угол, отвечающий q, есть 2psin qdq; отсюда

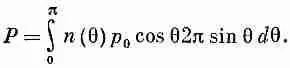
(11.19)

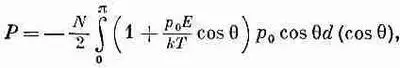
Подставляя вместо n(q) его выражение из (11.17), имеем

что легко интегрируется и приводит к следующему результату:

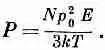
(11.20)

Поляризация пропорциональна полю Е, поэтому диэлектри­ческие свойства будут обычные. Кроме того, как мы и ожидаем, поляризация обратно пропорциональна температуре, потому что при более высоких температурах столкновения больше разрушают выстроенность. Эта зависимость вида 1/ T называется законом Кюри. Квадрат постоянного момента р 0 появляется по следующей причине: в данном электрическом поле выстраиваю­щая сила зависит от р 0, а средний момент, возникающий при выстраивании, снова пропорционален р 0 . Средний индуцируе­мый момент пропорционален р 0 2

Теперь посмотрим, насколько хорошо уравнение (11.20) согласуется с экспериментом. Возьмем водяной пар. Поскольку мы не знаем, чему равно р 0 , то не можем прямо вычислить и Р, но уравнение (11.20) предсказывает, что x- 1 должна ме­няться обратно пропорционально температуре, и это нам сле­дует проверить.

Из (11.20) получаем

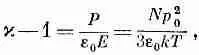
(11.21)

так что x-1 должна меняться прямо пропорционально плот­ности N и обратно пропорционально абсолютной температуре. Диэлектрическая проницаемость была измерена при несколь­ких значениях давления и температуры, выбранных таким об­разом, чтобы число молекул в единице объема оставалось постоянным. (Заметим, что, если бы все измерения выполнялись при постоянном давлении, число молекул в единице объема уменьшалось бы линейно с повышением температуры, а х-1 изменялась бы как T -2, а не как T -1.)

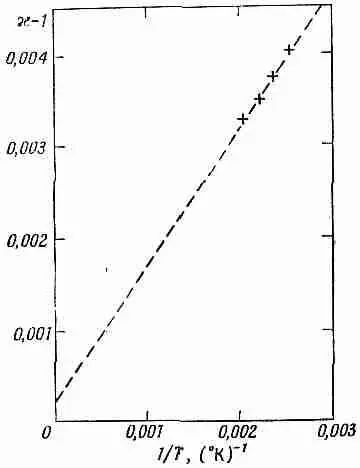
Фиг. 11.4. Измеренные значе­ния диэлектрической проницае­мости водяного пара при не­скольких температурах.

На фиг. 11.4 мы отложили измеренные значения к — 1 как функ­цию 1/T. Зависимость, предсказываемая форму­лой (11.21), выполняется хорошо.

Есть еще одна особен­ность диэлектрической проницаемости полярных молекул — ее изменение в зависимости от частоты внешнего поля. Благодаря тому что молекулы имеют момент инерции, тяжелым молекулам тре­буется определенное время, чтобы повернуться в направлении поля. Поэтому, если использовать частоты из верхней микро­волновой зоны или из еще более высокой, полярный вклад в диэлектрическую проницаемость начинает спадать, так как молекулы не успевают следовать за полем. В противополож­ность этому электронная поляризуемость все еще остается неизменной вплоть до оптических частот, поскольку инерция

электронов меньше.

§ 4. Электрические поля в пустотах диэлектрика

Теперь мы переходим к интересному, но сложному вопросу о диэлектрической проницаемости плотных веществ. Возьмем, например, жидкий гелий, или жидкий аргон, или еще какое-нибудь неполярное вещество. Мы по-прежнему ожидаем, что у них есть электронная поляризуемость. Но в плотных средах значение Р может быть велико, поэтому в поле, действующее на отдельный атом, вклад будет давать поляризация атомов, находящихся по соседству. Возникает вопрос, чему равно электрическое поле, действующее на отдельный атом?

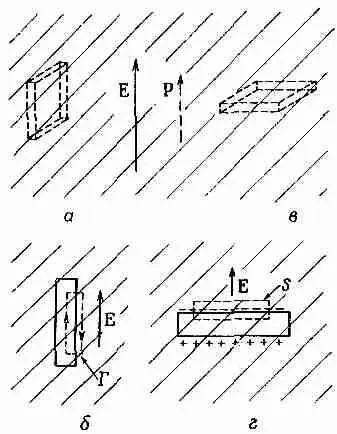
Фиг. 11.5. Поле внутри щели, вырезанной в диэлектрике, за­висит от ее формы, и ориента­ции.

Вообразите, что между пластинами конденсатора находится жидкость. Если пластины заряжены, они создадут в жидкости элек­трическое поле. Но каждый атом имеет заряды, и пол­ное поле Е есть сумма обоих этих вкладов. Это истинное электрическое поле в жидкости меняется очень-очень быстро от точки к точке. Оно чрезвычайно велико внутри атомов, особенно вблизи ядра, и сравнительно мало между атомами. Разность потенциалов между пластинами есть интеграл от этого полного поля. Если мы пренебрежем всеми быстрыми изменениями, то можем представить себе некое среднее электрическое поле Е, равное как раз V/d. (Именно это поле мы исполь­зовали в предыдущей главе.) Это поле мы должны себе пред­ставлять как среднее по пространству, содержащему много атомов.

Вы можете подумать, что «средний» атом в «среднем» поло­жении почувствует именно это среднее поле. Но все не так просто, и в этом можно убедиться, представив, что в диэлект­рике имеются отверстия разной формы. Предположим, что мы вырезали в поляризованном диэлектрике щель, ориентирован­ную параллельно полю (фиг. 11.5, а). Поскольку мы знаем, что СXE = 0, то линейный интеграл от Е вдоль кривой Г, на­правленной так, как показано на фиг. 11.5, б, должен быть равен нулю. Поле внутри щели должно давать такой вклад, который в точности погасит вклад от поля вне щели. Поэтому поле E 0в центре длинной тонкой щели равно Е, т.е. среднему электрическому полю, найденному в диэлектрике.

Рассмотрим теперь другую щель, повернутую своей ши­рокой стороной перпендикулярно Е (фиг. 11.5, в). В этом случае поле e 0в щели не совпадает с Е, потому что на стенках щели возникают поляризационные заряды. Применив закон Гаусса к поверхности S, изображенной на фиг. 11.5, г, мы находим, что поле Е йвнутри щели дается выражением

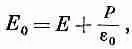
(11.22)

где Е, как и раньше,— электрическое поле в диэлектрике. (Гауссова поверхность охватывает поверхностный поляриза­ционный заряд s пол= Р.) Мы отмечали в гл. 10, что e 0 Е + Р часто обозначают через D, поэтому e 0Е 0= D 0равно величине D в диэлектрике.

В ранний период истории физики, когда считалось очень важным определять каждую величину прямым экспериментом, физики были очень довольны, обнаружив, что они могут опре­делить то, что понимают под Е и D в диэлектрике, не ползая в промежутках между атомами. Среднее поле Е численно равно полю Е 0, измеренному в щели, параллельной полю. А поле D могло быть измерено с помощью Е 0 , найденной в щели, перпен­дикулярной полю. Но никто эти поля никогда не измерял (таким способом, во всяком случае), так что это одна из многих бесплодных проблем.