Ричард Фейнман - 5. Электричество и магнетизм

Уравнение диффузии появляется во многих физических задачах: о диффузии газов, диффузии нейтронов и других. Мы уже обсуждали физику некоторых таких явлений в вып. 4, гл. 43. Теперь перед вами полное уравнение, описывающее диффузию в самом общем виде. Немного позже мы зай­мемся решением уравнения диффузии, чтобы посмотреть, как распределяется температура в некоторых случаях. А сейчас вернемся к рассмотрению других теорем о векторных полях.

§ 5. Циркуляция векторного поля

Мы хотим теперь рассмотреть ротор поля примерно так же, как рассматривали дивергенцию. Мы вывели теорему Гаусса, вычисляя интеграл по поверхности, хотя с самого начала отнюдь не было ясно, что мы будем иметь дело с дивергенцией. Откуда же можно было знать, что для ее получения надо интегрировать по поверхности? Этот результат вовсе не был очевиден. И столь же неоправданно мы сейчас вычислим другую характе­ристику поля и покажем, что она связана с ротором. На этот раз мы подсчитаем так называемую циркуляцию векторного поля. Если С — произвольное векторное поле, мы возьмем его составляющую вдоль кривой линии и проинтегрируем эту составляющую по замкнутому контуру. Интеграл называется циркуляцией векторного поля по контуру. Мы уже раньше в этой главе рассматривали криволинейный интеграл от Сy. Сейчас мы то же самое проделываем с произвольным векторным полем С.

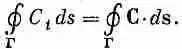
Пусть Г — произвольный замкнутый контур в пространстве (воображаемый, разумеется). Пример мы видим на фиг. 3.7. Криволинейный интеграл от касательной составляющей С по контуру записывается в виде

(3.30)

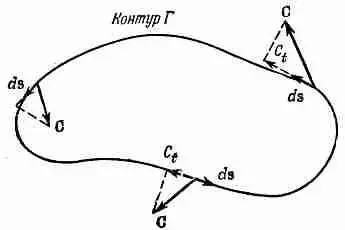
Фиг. 3.7. Циркуляция вектора С но кривой Г есть криволиней­ный интеграл от С t (касатель­ной составляющей С).

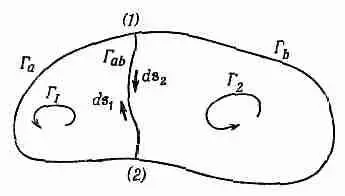
Фиг. 3.8. Циркуляция по всему контуру есть сумма циркуляции по двум контурам: Г 1 =Г a +Г ab и Г 2 =Г ь +Г a Ь .

Заметьте, что интеграл берется по всему замкнутому пути, а не от одной точки до другой, как это делалось раньше. Кру­жочек на знаке интеграла должен нам напоминать об этом. Такой интеграл называется циркуляцией векторного поля по кривой Г. Название связано с тем, что первоначально так рас­считывали циркуляцию жидкости. Но название это, как и по­ток, было распространено на любые поля, даже такие, в которых «циркулировать» нечему.

Забавляясь той же игрой, как с потоком, мы можем пока­зать, что циркуляция вдоль контура есть сумма циркуляции вдоль двух меньших контуров. Положим, что, соединив две точки (1) и (2) первоначальной кривой с помощью некоторой линии, мы разбили кривую на два контура Г 1и Г 2(фиг. 3.8). Контур Г 1состоит из Г a— части первоначальной кривой слева от (1) и (2) и «соединения» Г ab . Контур Г 2состоит из остатка первоначальной кривой плюс то же соединение.

Циркуляция вдоль Г 1есть сумма интеграла вдоль Г аи вдоль Г аЬ. Точно так же и циркуляция вдоль Г 2есть сумма двух ча­стей, одной вдоль Г b, другой — вдоль Г ab. Интеграл вдоль Г ab для кривой Г 2имеет знак, противоположный тому знаку, кото­рый он имел для кривой Г 1 , потому что направления обхода противоположны (в обоих криволинейных интегралах направ­ления поворота нужно брать одни и те же).

Повторяя прежние аргументы, мы можем убедиться, что сумма двух циркуляции даст как раз криволинейный интеграл вдоль первоначальной кривой Г. Интегралы по Г abсократятся. Циркуляция по одной части плюс циркуляция вдоль другой равняется циркуляции вдоль внешней линии. Этот процесс раз­резания большого контура на меньшие можно продолжить. При сложении циркуляции по меньшим контурам смежные части будут сокращаться, так что сумма их сведется к цирку­ляции вдоль единственного первоначального контура.

Теперь предположим, что первоначальный контур — это граница некоторой поверхности. Существует бесконечное мно­жество поверхностей, границей которых служит все тот же первоначальный замкнутый контур. Наши результаты не зави­сят, однако, от выбора этих поверхностей. Сперва мы разобьем наш первоначальный контур на множество малых контуров, лежащих на выбранной поверхности (фиг. 3.9).

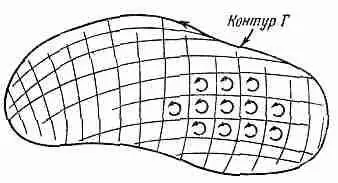
Фиг. 3.9. Некоторая поверх­ность, ограниченная конту­ром Г.

Поверхность разделена на множе­ство маленьких участков, каждый примерно в форме квадрата. Цир­куляция по Г есть сумма циркуля­ции по всем маленьким контурам.

Какой бы ни была форма поверхности, но если малые контуры сделать до­статочно малыми, всегда можно будет считать каждый из них замыкающим достаточно плоскую поверхность. Кроме того, каждый из них можно сделать очень похожим на квадрат. И циркуляцию вокруг большого контура Г можно найти, под­считав циркуляции по всем квадратикам и сложив их.

§ 6. Циркуляция по квадрату; теорема Стокса

Как нам найти циркуляцию по каждому квадратику? Все зависит от того, как квадрат ориентирован в пространстве. Если ориентация его подобрана удачно (к примеру, он распо­ложен в одной из координатных плоскостей), то расчет сде­лать легко. Так как пока мы не делали никаких предположений об ориентации осей координат, мы вправе выбрать их так, чтобы тот квадратик, на котором мы сосредоточили свое вни­мание, оказался в плоскости ху (фиг. 3.10). Если результат расчета будет выражен в векторной записи, то можно говорить, что он не зависит от специальной ориентации плоскости.

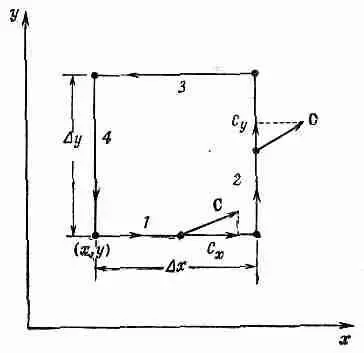
Фиг. 3.10. Вычисление цирку­ляции вектора С по маленькому квадратику.

Мы хотим теперь найти циркуляцию поля С по нашему квад­ратику. Криволинейное интегрирование легко проделать, если квадратик сделать таким маленьким, чтобы вектор С на про­тяжении одной стороны квадрата менялся очень мало. (Это предположение выполняется тем лучше, чем меньше квадратик, так что на самом деле речь идет о бесконечно малых квадра­тиках.) Отправившись от точки (х, у) — в левом нижнем углу фигуры,— мы обойдем весь квадрат в направлении, указанном стрелками. Вдоль первой стороны, отмеченной цифрой 1, ка­сательная составляющая равна С х (1),а расстояние равно Dx. Первая часть интеграла равна C x(1) Dx, Вдоль второй стороны получится С у(2) Dy. Вдоль третьей мы получим -С x(3) Dx, а вдоль четвертой -C y(4) Dy. Знаки минус стоят потому, что нас интересует касательная составляющая в направлении об­хода. Весь криволинейный интеграл тогда равен